
【题目】对于数轴上的A、B、C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“至善点”.例如:若数轴上点A、B、C所表示的数分别为1、3、4,则点B是点A、C的“至善点”.
(1)若点A表示数﹣2,点B表示数2,下列各数![]() 、0、1、6所对应的点分别为C1、C2、C3、C4,其中是点A、B的“至善点”的有 (填代号);
、0、1、6所对应的点分别为C1、C2、C3、C4,其中是点A、B的“至善点”的有 (填代号);
(2)已知点A表示数﹣1,点B表示数3,点M为数轴上一个动点:
①若点M在点A的左侧,且点M是点A、B的“至善点”,求此时点M表示的数m;
②若点M在点B的右侧,点M、A、B中,有一个点恰好是其它两个点的“至善点”,求出此时点M表示的数m.
【答案】(1)C1、C4;(2)①﹣5;②点M表示的数m可以为5,7,11
【解析】
(1)根据C1、C2、C3、C4所表示的数,分别计算这个点到A、B的距离,根据“至善点”的意义进行判断即可;
(2)①点M在点A的左侧,则m<﹣1,点M是点A、B的“至善点”,则有2MA=MB,列方程求解即可;
②点M在点B的右侧,则m>3,由点M、A、B中,有一个点恰好是其它两个点的“至善点”,分三种情况进行讨论: M是A、B的“至善点”,A是B、M的“至善点”,B是A、M的“至善点”,分别建立方程即可求解.
解:(1)当C1=﹣![]() 时,AC1=|﹣
时,AC1=|﹣![]() +2|=
+2|=![]() ,BC1=|2+
,BC1=|2+![]() |=
|=![]() ,有BC1=2AC1,因此C1符合题意;
,有BC1=2AC1,因此C1符合题意;
当C2=0时,AC2=|0+2|=2,BC2=|2+0|=2,有BC2=AC2,因此C2不符合题意;
当C3=1时,AC3=|1+2|=3,BC3=|2﹣1|=1,有3BC3=AC3,因此C3不符合题意;
当C4=6时,AC4=|6+2|=8,BC4=|2﹣6|=4,有2BC4=AC4,因此C4符合题意;
故答案为:C1、C4;
(2)①点M在点A的左侧,则m<﹣1,
点M是点A、B的“至善点”,因此有2MA=MB,即2(﹣1﹣m)=3﹣m,
解得,m=﹣5,
②点M在点B的右侧,则m>3,
点M、A、B中,有一个点恰好是其它两个点的“至善点”,
Ⅰ)若M是A、B的“至善点”,则2MB=MA,即2(m﹣3)=m+1,解得m=7,
Ⅱ)若A是B、M的“至善点”,则2AB=AM,即2(3+1)=m+1,解得m=7,
Ⅲ)若B是A、M的“至善点”,则2AB=BM或AB=2BM,即2(3+1)=m﹣3或3+1=2(m﹣3),解得m=11或m=5,
答:点M表示的数m可以为5,7,11.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
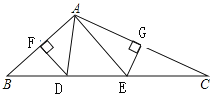
【题目】如图,△ABC中,AB,AC边的垂直平分线分别交BC于点D,E,垂足分别为点F,G,△ADE的周长为6cm
(1)求△ABC中BC边的长度;(2)若∠B+∠C=64°,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
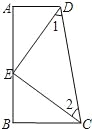
【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)Rt△ADE与Rt△BEC全等吗?请写出必要的推理过程;
(2)△CED是不是直角三角形?请说明理由;
(3)若已知AD=6,AB=14,请求出请求出△CED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价1200元,领带每条定价140元.厂方在开展促销活动期间,可以同时向客户提供两种优惠方案:
①买一套西装送一条领带
②西装和领带都按定价的![]() 付款,现某客户要到该服装厂购买西装20套,领带
付款,现某客户要到该服装厂购买西装20套,领带![]() 条(
条(![]() 超过20)
超过20)
(1)若该客户按方案①购买,需付款_________元(用含![]() 的式子表示);若该客户按方案②购买,需付款_________元(用含
的式子表示);若该客户按方案②购买,需付款_________元(用含![]() 的式子表示)
的式子表示)
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
(3)若![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
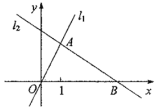
【题目】如图,在平面直角坐标系xOy中,点A(m,2)在直线![]() :y=2x上,过点A的直线
:y=2x上,过点A的直线![]() 与x轴交于点B(4,0).
与x轴交于点B(4,0).
(1)求直线![]() 的解析式;
的解析式;
(2)己知点P.的坐标为(n,0),过点P垂直x轴的直线与![]() ,
,![]() 分别交于点C,D,当点C位于点D上方时,求n的取值范围.
分别交于点C,D,当点C位于点D上方时,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2,动点P从点B出发,以每秒1个单位的速度在正方形的边上沿BC-CD-DA运动,设运动时间为t,△PAB面积为S.

(1)求S关于t的函数解析式,并写出自变量t的取值范围;
(2)画出相应函数图象;
(3)当S=![]() 时,t的值为多少.
时,t的值为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题,求![]() 的立方根.华罗庚脱口而出,你知道怎样迅速准确地计算出结果的吗?请按照下面的问题试一试:
的立方根.华罗庚脱口而出,你知道怎样迅速准确地计算出结果的吗?请按照下面的问题试一试:
(1)由![]() ,确定
,确定![]() 的立方根是 位数;
的立方根是 位数;
(2)由![]() 的个位数是
的个位数是![]() 确定
确定![]() 的立方根的个位数是 ;
的立方根的个位数是 ;
(3)如果划去![]() 后面的三位
后面的三位![]() 得到数
得到数![]() ,而
,而![]() ,由此能确定
,由此能确定![]() 的立方根的十位数是 ;所以
的立方根的十位数是 ;所以![]() 的立方根是 ;
的立方根是 ;
(4)用类似的方法,请说出![]() 的立方根是 .
的立方根是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
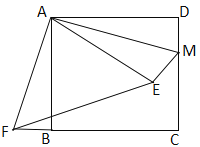
【题目】如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为( )
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com