
【题目】如图,在边长都为 a 的正方形内分别排列着一些大小相等的圆:
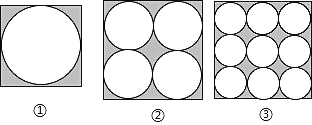
(1)根据图中的规律,第 4 个正方形内圆的个数是 ,第n 个正方形内圆的个数是_____.
(2)如果把正方形内除去圆的部分都涂上阴影.
①用含a 的代数式分别表示第 1 个正方形中、第 3 个正方形中阴影部分的面积(结果保留π);
②若 a=10,请直接写出第 2018 个正方形中阴影都分的面积 (结果保留π)
【答案】(1)16,n2(2)100﹣25π
【解析】
(1)观察上图可知第①个图形圆的个数是 12=1,第②个图形圆的个数是22=4,第③个图形圆的个数是 32=9,第④个图形圆的个数是 42=16,…,可知第 n 个正方形中圆的个数为 n2 个;
(2)阴影部分的面积等于正方形的面积减去圆的面积,由此列式后即可得到答案;从而推广运用得到结论.
(1)观察上图可知第①个图形圆的个数是12=1,
第②个图形圆的个数是22=4,
第③个图形圆的个数是32=9,
第④个图形圆的个数是42=16,
…,
可知第n个正方形中圆的个数为n2个;
故答案为:16,n2;
(2)①第一个S阴影=a2﹣π(![]() )2=
)2= ![]() a2;
a2;
第二个S阴影=a2﹣4π(![]() )2=
)2= ![]() a2;
a2;
第三个S阴影=a2﹣9π(![]() )2=
)2= ![]() a2;
a2;
②从以上计算看出三个图形中阴影部分的面积均相等,与圆的个数无关.
第n图形中阴影部分的面积是S阴影=a2﹣n2π(![]() )2=
)2= ![]() a2;
a2;
当 a=10,第 2018 个阴影部分的面积为![]() ×102=100﹣25π.
×102=100﹣25π.
故答案为:100﹣25π.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】当前正值樱桃销售季节,小李用20000元在樱桃基地购进樱桃若干进行销售,由于销售状况良好,他又立即拿出60000元资金购进该种樱桃,但这次的进货价比第一次的进货价提高了20%,购进樱桃数量是第一次的2倍还多200千克.
(1)该种樱桃的第一次进价是每千克多少元?
(2)如果小李按每千克90元的价格出售,当大部分樱桃售出后,余下500千克按售价的7折出售完,小李销售这种樱桃共盈利多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设计一个商标图形(如图8所示),在△ABC中,AB=AC=2cm,∠B=30°,以A为圆心,AB为半径作 ![]() ,以BC为直径作半圆
,以BC为直径作半圆 ![]() ,则商标图案(阴影)面积等于cm2 .
,则商标图案(阴影)面积等于cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,8),B(﹣4,0),线段AB的垂直平分线CD分别交AB、OA于点C、D,其中点D的坐标为(0,3).
(1)求直线AB的解析式;
(2)求线段CD的长;
(3)点E为y轴上一个动点,当△CDE为等腰三角形时,求E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点![]() ,
,![]() 若对于平面内一点C,当
若对于平面内一点C,当![]() 是以AB为腰的等腰三角形时,称点C时线段AB的“等长点”.
是以AB为腰的等腰三角形时,称点C时线段AB的“等长点”.
![]() 请判断点
请判断点![]() ,点
,点![]() 是否是线段AB的“等长点”,并说明理由;
是否是线段AB的“等长点”,并说明理由;
![]() 若点
若点![]() 是线段AB的“等长点”,且
是线段AB的“等长点”,且![]() ,求m和n的值.
,求m和n的值.
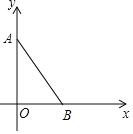
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )
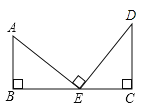
A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为 . 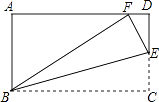
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com