
【题目】某区教育系统为了更好地宣传扫黑除恶专项斗争,印制了应知应会手册,该区教育局想了解教师对扫黑除恶专项斗争应知应会知识掌握程度,抽取了部分教师进行了测试,并将测试成绩绘制成下面两幅统计图,请根据统计图中提供的信息,回答下面问题:
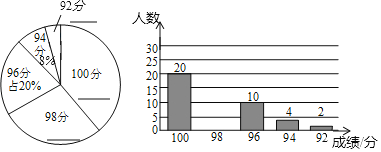
(1)计算样本中,成绩为98分的教师有 人,并补全两个统计图;
(2)样本中,测试成绩的众数是 ,中位数是 ;
(3)若该区共有教师6880名,根据此次成绩估计该区大约有多少名教师已全部掌握扫黑除恶专项斗争应知应会知识?
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.
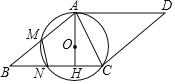
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
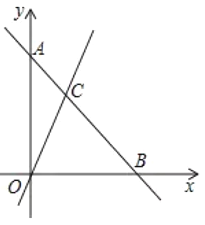
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 沿路线
沿路线![]() 运动.
运动.
(1)求直线![]() 的解析式;
的解析式;
(2)设![]() 的面积
的面积![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求出
,求出![]() 与
与![]() 的关系式;
的关系式;
(3)是否存在点![]() ,使
,使![]() 是直角三角形?若存在,直接写出点
是直角三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:数学课上,老师出示了这样一个问题:
如图1,在等边![]() 中,点
中,点![]() 、
、![]() 在
在![]() 上,且
上,且![]() ,直线
,直线![]() 交
交![]() 于
于![]() 点,交
点,交![]() 延长线于
延长线于![]() 点,且
点,且![]() ,探究线段
,探究线段![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 存在某种数量关系”;
存在某种数量关系”;
小强:“通过观察和度量,发现图1中有一条线段与![]() 相等”;
相等”;
小伟:“通过构造三角形,证明三角形全等,进而可以得到线段![]() 之间的数量关系”.
之间的数量关系”.
……
老师:“保留原题条件,再过点![]() 作
作![]() 交
交![]() 于
于![]() 与
与![]() 相交于点
相交于点![]() (如图2)如果给出
(如图2)如果给出![]() 的值,那么可以求出
的值,那么可以求出![]() 的值”.
的值”.
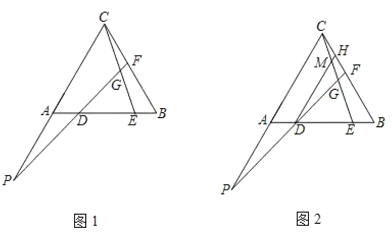
请回答:
(1)在图1中找出![]() 与
与![]() 数量关系,并证明;
数量关系,并证明;
(2)在图1中找出与线段![]() 相等的线段,并证明;
相等的线段,并证明;
(3)探究线段![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(4)若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法错误的是( )
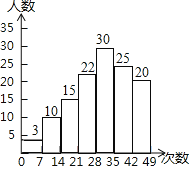
A.这栋居民楼共有居民125人
B.每周使用手机支付次数为28~35次的人数最多
C.有的人每周使用手机支付的次数在35~42次
D.每周使用手机支付不超过21次的有15人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上运动,且
上运动,且![]() .连接
.连接![]() ,作
,作![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .
.
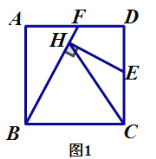

(1)如图1,若点![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 之间的数量关系是______;
之间的数量关系是______;
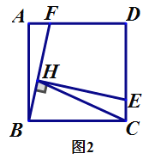
(2)如图2,当点![]() 在
在![]() 边上且不是
边上且不是![]() 的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上运动时,连接
上运动时,连接![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位运动员在相同条件下各射击![]() 次,成绩如下: 甲:
次,成绩如下: 甲:![]() ; 乙:
; 乙:![]() 根据上述信息,下列结论错误的是( )
根据上述信息,下列结论错误的是( )
A.甲、乙的众数分别是![]() B.甲、乙的中位数分别是
B.甲、乙的中位数分别是![]()
C.乙的成绩比较稳定D.甲、乙的平均数分别是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com