

分析 (1)根据条件可以得出△BDH≌△ADC就可以得出BH=AC;
(2)先根据条件画出图形,再证明△BDH≌△ADC就可以得出结论.
解答 解:
(1)BH=AC.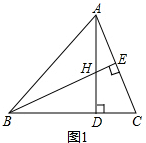
理由:∵AD⊥BC,BE⊥AC,
∴∠ADB=∠ADC=∠AEB=∠BEC=90°,
∴∠CBE+∠C=90°,∠DAC+∠C=90°,
∴∠CBE=∠DAC.
∵∠ABC=45°,
∴∠BAD=45°,
∴∠ABC=∠BAD,
∴BD=AD.
在△BDH和△ADC中
$\left\{\begin{array}{l}{∠CBE=∠DAC}\\{BD=AD}\\{∠ADB=∠ADC}\end{array}\right.$,
∴△BDH≌△ADC(ASA),
∴BH=AC;
(2)成立,BH=AC.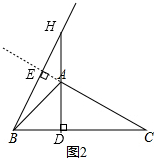
理由:如图2,∵AD⊥BC,BE⊥AC,
∴∠ADB=∠ADC=∠AEB=∠AEH=90°,
∴∠CBE+∠C=90°,∠CBE+∠DHB=90°,
∴∠DHB=∠C.
∵∠ABC=45°,
∴∠BAD=45°,
∴∠ABC=∠BAD,
∴BD=AD.
在△BDH和△ADC中
$\left\{\begin{array}{l}{∠BHD=∠C}\\{BD=AD}\\{∠ADB=∠ADC}\end{array}\right.$,
∴△BDH≌△ADC(ASA),
∴BH=AC.
点评 本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.


科目:初中数学 来源: 题型:解答题
 搭一搭,算一算;
搭一搭,算一算;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查宇宙飞船“神舟九号”的零部件 | B. | 调查一批飞行员的视力 | ||
| C. | 调查八年级(下)语文书的排版正确率 | D. | 调查市民对“闯红灯”的认识状况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是( )
如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是( )| A. | π cm2 | B. | 2π cm2 | C. | 4π cm2 | D. | 8π cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在如图所示的直角坐标系xOy中有一线段AB,其中A和B均在坐标轴上且AB=4,点P(x,y)是AB的中点.现将AB进行移动,但仍保持AB=4,则x,y应满足的关系是( )
在如图所示的直角坐标系xOy中有一线段AB,其中A和B均在坐标轴上且AB=4,点P(x,y)是AB的中点.现将AB进行移动,但仍保持AB=4,则x,y应满足的关系是( )| A. | x2+y2=1 | B. | x+y=1 | C. | x2+y2=4 | D. | x+y=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20%a元 | B. | (1-20%)a元 | C. | (1+20%)a元 | D. | $\frac{a}{1+20%}$元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com