
【题目】已知关于x的一元二次方程(m﹣1)x2+(m﹣2)x﹣1=0(m为实数).
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)若m是整数,且方程有两个不相等的整数根,求m的值.
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
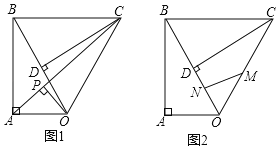
【题目】已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,连接BC
(1)如图1,连接AC,作OP⊥AC,垂足为P,求△AOC的面积和线段OP的长;
(2)如图2,点M是线段OC的中点,点N是线段OB上的动点(不与点O重合),求△CMN周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
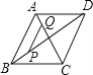
【题目】如图所示,在ABCD中,AB=AC=4,BD=6,P是线段BD上任意一点,过点P作PQ∥AB,与AC交于点Q,设BP=x,PQ=y,则能反映y与x之间关系的图象为( )
A.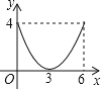 B.
B.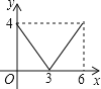 C.
C.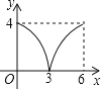 D.
D.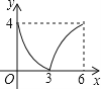
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-2,1),B(0,4),C(8,16),O(0,0),P(m,n),抛物线y=ax2(a≠0)经过A,B,C,其中的一点,
(1)求抛物线y=ax2(a≠0)的解析式;
(2)若直线y=mx(m≠0)与直线y=nx(n≠0)分别经过点A与点C,判断点P(m,n)是否在反比例函数y=-![]() 的图象上;
的图象上;
(3)若点P(m,n)是反比例函数y=-![]() 的图象上任一点,且直线y=mx(m≠0)与直线y=nx(n≠0)分别与抛物线y=ax2(a≠0)交于点M,点N(不同于原点),求证:M,B,N三点在一条直线上.
的图象上任一点,且直线y=mx(m≠0)与直线y=nx(n≠0)分别与抛物线y=ax2(a≠0)交于点M,点N(不同于原点),求证:M,B,N三点在一条直线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在Rt△ABC中,∠ACB=90°,AC=6cm,动点P从点B出发,沿折线B→A→C路线匀速运动到C停止,动点Q从点C出发,沿折线C→B→A路线匀速运动到A停止,如点P、Q同时出发运动t秒后,如图(2)是△BPC的面积S1(cm2)与t(秒)的函数关系图象,图(3)是△AQC的面积S2(cm2)与t(秒)的函数关系图象:
(1)点P运动速度为 cm/秒;Q运动的速度 cm/秒;
(2)连接PQ,当t为何值时,PQ∥BC;
(3)如图(4)当运动t(0≤t≤2)秒时,是否存在这样的时刻,使以PQ为直径的⊙O与Rt△ABC的一条边相切,若存在,求出t的值;若不存在,请说明理由.
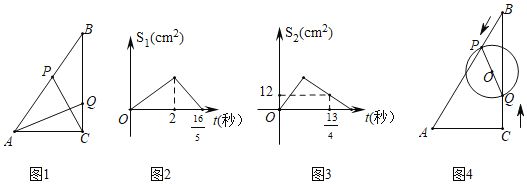
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点坐标为![]() ,直线
,直线![]() 与二次函数的图象交于
与二次函数的图象交于![]() ,
,![]() 两点,其中
两点,其中![]() 点的坐标为
点的坐标为![]() ,
,![]() 点在
点在![]() 轴上.
轴上.
(1)求![]() 的值及这个二次函数的解析式;
的值及这个二次函数的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的周长最小,并求出此时
的周长最小,并求出此时![]() 点坐标;
点坐标;
(3)若![]() 是
是![]() 轴上的一个动点,过
轴上的一个动点,过![]() 作
作![]() 轴的垂线分别于直线
轴的垂线分别于直线![]() 和二次函数的图象交于
和二次函数的图象交于![]() ,
,![]() 两点.当
两点.当![]() 时,求线段
时,求线段![]() 的最大值;
的最大值;
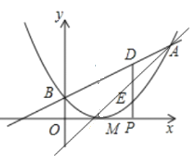
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少( )个时,网球可以落入桶内.
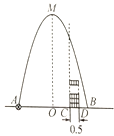
A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A,B,C,D都在边长为1的小正方形网格的格点上,过点M(1,-2)的抛物线y=mx2+2mx+n(m>0)可能还经过( )
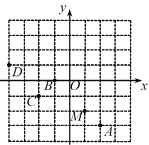
A.点AB.点BC.点CD.点D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com