
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ6����B��ʾ����Ϊ��4��CΪ�߶�AB���е㣬����P�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮![]()
��1����C��ʾ��������
��2����t=��ʱ����P�����A����
��3����P��ʾ���������ú���ĸt�Ĵ���ʽ��ʾ����
��4����t=��ʱ���߶�PC�ij�Ϊ2����λ���ȣ�
��5��������Qͬʱ�ӵ�A��������ÿ��1����λ���ȵ��ٶ����������������˶�����ô����t=��ʱ��PQ�ij�Ϊ1����λ���ȣ�
���𰸡�
��1��1
��2��5
��3��2t��4
��4��1.5���3.5��
��5��3��� ![]() ��
��
���������⣺��1����6��4����2=2��2=1���ʵ�C��ʾ������1���ʴ�Ϊ��1��
��2��[6������4��]��2
=10��2
=5���룩��
�𣺵�t=5��ʱ����P�����A����
�ʴ�Ϊ��5��
��3����P��ʾ������2t��4��
�ʴ�Ϊ��2t��4��
��4��P�ڵ�C��ߣ�
[1��2������4��]��2
=3��2
=1.5���룩��
P�ڵ�C�ұߣ�
[1+2������4��]��2
=7��2
=3.5���룩��
�𣺵�t=1.5���3.5����ʱ���߶�PC�ij�Ϊ2����λ���ȣ�
�ʴ�Ϊ��1.5���3.5�룻
��5����P��Q����ǰ����������
��2+1��t=6������4����1��
���t=3��
��P��Q��������������
��2+1��t=6������4��+1��
���t= ![]() ��
��
�𣺵�t=3��� ![]() ����ʱ��PQ�ij�Ϊ1����λ���ȣ�
����ʱ��PQ�ij�Ϊ1����λ���ȣ�
�ʴ�Ϊ��3��� ![]() �룮
�룮
��1�������߶��е����깫ʽ�����C��ʾ��������2������ʱ��=·�̡��ٶȣ�����t��ֵ����3����������֮��ľ��빫ʽ�����P��ʾ��������4����P�ڵ�C��ߺ͵�C�ұ��������������⣻��5���ֵ�P��Q����ǰ�͵�P��Q�������������������⣮


 Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д� ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������һ�鳤Ϊ20�ף���Ϊ12�ij��������أ����ڽ�������������������x��С·���м����µij����β������˵أ��ô���ʽ��ʾ�� 
��1���˵صij�a=�ף���b=�ף�
��2���˵ص����S=ƽ���ף�
��3����x=2��ʱ���˵ص������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������в���ʽ���飩�����ѽ⼯�������ϱ�ʾ������
��1��![]() ��5��x
��5��x
��2��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��4ac��b2��
������![]() ����������x1=��1��x2=3��
����������x1=��1��x2=3��
��3a+c��0
����y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3
����x��0ʱ��y��x���������
���н�����ȷ�ĸ����ǣ�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������κϽ��ĵijɱ�y(Ԫ)��������������ȣ���߳�Ϊxcm.��x��3ʱ��y��18����ô���ɱ�Ϊ72Ԫʱ���߳�Ϊ�� ��
A. 6cmB. 12cmC. 24cmD. 36cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ģ�Ѱ�ҹ��ɣ�
���㣺��1��x����1+x��=1��x2 �� ��1��x����1+x+x2��=1��x3 �� ��1��x����1+x+x2+x3��=1��x4����
��1���۲���ʽ�������룺��1��x����1+x+x2+��+xn��= ��
��2��������IJ��룬���㣺1+3+32+33��+3n= �� ������n����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c����A��1��0����B��4��0����C��0��3��������
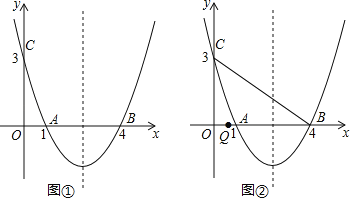
��1���������ߵĽ���ʽ��
��2����ͼ�����������ߵĶԳ������Ƿ���ڵ�P��ʹ���ı���PAOC���ܳ���С�������ڣ�����ı���PAOC�ܳ�����Сֵ���������ڣ���˵��������
��3����ͼ������Q���߶�OB��һ���㣬����BC�����߶�BC���Ƿ���������ĵ�M��ʹ��CQMΪ��������������BQMΪֱ�������Σ������ڣ����M�����ꣻ�������ڣ���˵��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com