
【题目】扬州市“五个一百工程”在各校普遍开展,为了了解某校学生每天课外阅读所用的时间情况,从该校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如下不完整的频数分布表和频数分布直方图.
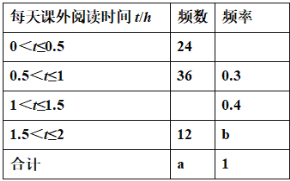
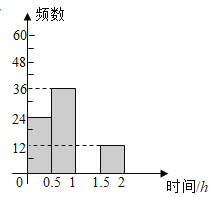
根据以上信息,请回答下列问题:
(1)表中a= ,b= ;
(2)请补全频数分布直方图;
(3)若该校有学生1200人,试估计该校学生每天阅读时间超过1小时的人数.
【答案】(1)120,0.1;(2)补全频数分布直方图见解析;(3)该校学生每天阅读时间超过1小时的人数为600人.
【解析】
(1)根据阅读时间在0.5<t≤1范围的频数与频率可求得a的值,继而用12除以a即可求得b的值;
(2)求出阅读时间在1<t≤1.5范围的人数,即可补全直方图;
(3)用1200乘以阅读时间超过1小时的频率即可求得答案.
(1)36÷0.3=120(人),总共120人,
∴a=120,
B=12÷120=0.1,
故答案为:120,0.1;
(2)0.4×120=48(人),
补全直方图如图所示:
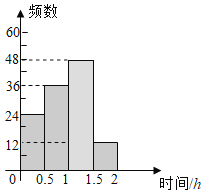
(3)1200×(0.4+0.1)=600人,
答:该校学生每天阅读时间超过1小时的人数为600人.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
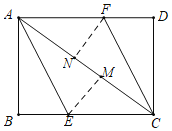
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
(2)当∠BAE为多少度时,四边形AECF是菱形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理![]() 、
、![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元;
型净水器的进价各是多少元;
(2)槐荫公司计划购进![]() 、
、![]() 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时![]() 型净水器每台售价2500元,
型净水器每台售价2500元,![]() 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售![]() 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献![]() 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,5×5正方形方格纸图中,点A,B都在格点处.
(1)请在图中作等腰△ABC,使其底边AC=2![]() ,且点C为格点;
,且点C为格点;
(2)在(1)的条件下,作出平行四边形ABDC,且D为格点,并直接写出平行四边形ABDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对几何命题进行逆向思考是几何研究中的重要策略,我们知道,等腰三角形两腰上的高 线相等,那么等腰三角形两腰上的中线,两底角的角平分线也分别相等吗?它们的逆命 题会正确吗?
(1)请判断下列命题的真假,并在相应命题后面的括号内填上“真”或“假”.
①等腰三角形两腰上的中线相等 ;
②等腰三角形两底角的角平分线相等 ;
③有两条角平分线相等的三角形是等腰三角形 ;
(2)请写出“等腰三角形两腰上的中线相等”的逆命题,如果逆命题为真,请画出图形,写出已知、求证并进行证明,如果不是,请举出反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现
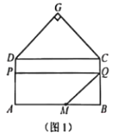
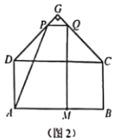
如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°,点M在线段AB上,且AM=a,点P沿折线AD-DG运动,点Q沿折线BC-CG运动(与点G不重合),在运动过程中始终保持线段PQ//AB.设PQ与AB之间的距离为x.
(1)若a=12.①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为_________;
②在运动过程中,求四边形AMQP的最大面积;
(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.


查看答案和解析>>
科目:初中数学 来源: 题型:
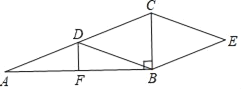
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送鲜花,感恩母亲,祝福母亲. 节日前夕,某花店采购了一批鲜花礼盒,成本价为30元每件,分析上一年母亲节的鲜花礼盒销售情况,得到了如下数据,同时发现每天的销售量![]() (件)是销售单价
(件)是销售单价![]() (元/件)的一次函数.
(元/件)的一次函数.
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 350 | 300 | 250 | 200 | … |
(1)求出![]() 与
与![]() 的函数关系;
的函数关系;
(2)物价局要求,销售该鲜花礼盒获得的利润不得高于100﹪:
①当销售单价![]() 取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价);
取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价);
②试确定销售单价![]() 取何值时,花店销该鲜花礼盒每天获得的利润
取何值时,花店销该鲜花礼盒每天获得的利润![]() (元)最大?并求出花店销该鲜花礼盒每天获得的最大利润.
(元)最大?并求出花店销该鲜花礼盒每天获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交于点
轴交于点![]() ,顶点坐标为
,顶点坐标为![]() .
.
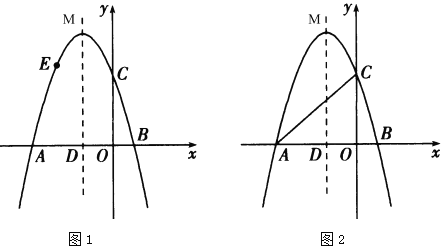
(1)求抛物线的表达式和顶点![]() 的坐标;
的坐标;
(2)如图1,点![]() 为抛物线上一点,点
为抛物线上一点,点![]() 不与点
不与点![]() 重合,当
重合,当![]() 时,过点
时,过点![]() 作
作![]() 轴,交抛物线的对称轴于点
轴,交抛物线的对称轴于点![]() ,作
,作![]() 轴于点H,得到矩形
轴于点H,得到矩形![]() ,求矩形
,求矩形![]() 的周长的最大值;
的周长的最大值;
(3)如图2,点![]() 为抛物线对称轴上一点,是否存在点
为抛物线对称轴上一点,是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形是直角三角形?若存在,求出点
为顶点的三角形是直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com