
【题目】如图,在梯形![]() 中,
中,![]() ,中位线
,中位线![]() 与对角线
与对角线![]() 交于
交于![]() 两点,若
两点,若![]() cm,
cm, ![]() cm,则
cm,则![]() 的长等于( )
的长等于( )

A. 10 cm B. 13 cm C. 20 cm D. 26 cm
科目:初中数学 来源: 题型:
【题目】某地下管道,若由甲队单独铺设,恰好在规定时间内完成;若由乙队单独铺设,需要超过规定时间15天才能完成,如果先由甲、乙两队合做10天,再由乙队单独铺设正好按时完成.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为5000元,乙队每天的施工费用为3000元,为了缩短工期以减少对居民交通的影响,工程指挥部最终决定该工程由甲、乙两队合做来完成,那么该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由两样大小的小圆圈按一定规律组成的,其中第①个图形中一共有7个小圆圈,第②个图形中一共有13个小圆圈,第③个图形中一共有21个小圆圈,…,按此规律排列,则第⑧个图形中小圆圈的个数为( )

A. 68 B. 88 C. 91 D. 93
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .若有一半径为
.若有一半径为![]() 的圆分别与
的圆分别与![]() 、
、![]() 相切,则下列何种方法可找到此圆的圆心( )
相切,则下列何种方法可找到此圆的圆心( )
A. ![]() 的角平分线与
的角平分线与![]() 的交点 B.
的交点 B. ![]() 的中垂线与
的中垂线与![]() 中垂线的交点
中垂线的交点
C. ![]() 的角平分线与
的角平分线与![]() 中垂线的交点 D.
中垂线的交点 D. ![]() 的角平分线与
的角平分线与![]() 中垂线的交点
中垂线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在![]() 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?
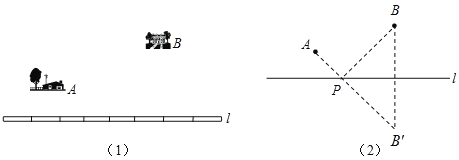
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
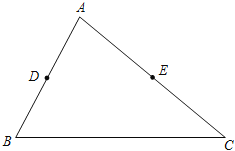
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3

(1)求证:BN=DN;
(2)求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1、2、3分别表示甲、乙、丙三人由A地到B地的路线图,已知
甲的路线为:A→C→B;
乙的路线为:A→D→E→F→B,其中E为AB的中点;
丙的路线为:A→I→J→K→B,其中J在AB上,且AJ>JB.

若符号[→]表示[直线前进],则根据图1、图2、图3的数据,判断三人行进路线长度的大小关系为( )
A. 甲=乙=丙 B. 甲<乙<丙 C. 乙<丙<甲 D. 丙<乙<甲
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校根据课程设置要求,开设了数学类拓展性课程. 为了解学生最喜欢的课程内容,随机抽取了部分学生进行问卷调查(每人必须且只选其中一项),并将统计结果绘制成如下统计图(不完整). 请根据图中信息回答问题:

(1)求![]() 的值.
的值.
(2)补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
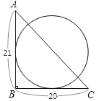
【题目】如图,已知![]() 、
、![]() 分别为
分别为![]() 的直径和弦,
的直径和弦,![]() 为
为![]() 的中点,
的中点,![]() 垂直于
垂直于![]() 的延长线于
的延长线于![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,下列结论一定错误的是( )
,下列结论一定错误的是( )

A. DE是⊙O的切线 B. 直径AB长为20cm
C. 弦AC长为16cm D. C为![]() 的中点
的中点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com