27ЁЂдФЖСЯТУцЕФВФСЯВЂНтД№ЮЪЬтЃЎ
ЭМаЮЪЧвЛжжживЊЕФЪ§бЇгябдЃЌЫќжБЙлаЮЯѓЃЌФмгааЇЕиБэЯжвЛаЉДњЪ§жаЕФЪ§СПЙиЯЕЃЎР§ШчЭъШЋЦНЗНЙЋЪНПЩвдгУЦНУцМИКЮЭМаЮЕФУцЛ§РДБэЪОЃЌЪЕМЪЩЯЛЙгавЛаЉДњЪ§КуЕШЪНвВПЩвдгУетжжаЮЪНБэЪОЃЌР§ШчЃЈ2a+bЃЉЃЈa+bЃЉ=2a
2+3ab+b
2ОЭПЩвдгУЭМ1ЛђЭМ2ЕШЭМаЮЕФУцЛ§БэЪОЃК



ЃЈ1ЃЉЧыаДГіЭМ3ЫљБэЪОЕФДњЪ§КуЕШЪНЃК
ЃЈa+2bЃЉЃЈ2a+bЃЉ=2a2+5ab+2b2
НтОіЮЪЬтЃК
ФГИжЬњМгЙЄГЇЯжгазуЙЛЕФ2ЁС2ЃЌ3ЁС3ЕФе§ЗНаЮКЭ2ЁС3ЕФОиаЮЯТНХСЯAЁЂBЁЂCЃЈШчЭМЫљЪОЃЉЃЌЯжДгжаИїбЁШЁШєИЩИіЯТНХСЯКИНгГЩВЛЭЌЕФЭМаЮЃЌЧыФудкЯТУцИјГіЕФЗНИёжНжаЃЌАДЯТСавЊЧѓЗжБ№ЛГівЛжжЪОвтЭМЃЈЫЕУїЃКЯТУцИјГіЕФЗНИёжНжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄОљЮЊ1ЃЌЦДГіЕФЭМаЮЃЌвЊЧѓУПСНИіЭМЦЌжЎМфМШЮоЗьЯЖЃЌвВЮожиЕўЃЌЛЭМБиаыБЃСєЦДНЯЕФКлМЃЃЉ
AЁЂ

BЁЂ

CЁЂ

ЃЈ2ЃЉбЁШЁAаЭ4ПщЃЌBаЭСНжжЭМЦЌ1ПщЃЌCаЭЭМЦЌ4ПщЃЌдкЯТУцЕФЭМ2жаЦДГЩвЛИіе§ЗНаЮЃЛ
РћгУУцЛ§ЗЈШЅНтЃЌШчЭМЫљЪОЃЎ

ЃЈ3ЃЉбЁШЁAаЭ3ПщЃЌBаЭСНжжЭМЦЌ1ПщЃЌCаЭЭМЦЌШєИЩПщЃЌдкЯТУцЕФЭМ3жаЦДГЩвЛИіГЄЗНаЮЃЎ






 BЁЂ
BЁЂ CЁЂ
CЁЂ


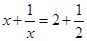 ЕФНтЮЊ
ЕФНтЮЊ ;
; ЕФНтЮЊ
ЕФНтЮЊ ;
; ЕФНтЮЊ
ЕФНтЮЊ ;
; ЕФНтЪЧ________________;
ЕФНтЪЧ________________; ЕФНтЪЧ___________________;
ЕФНтЪЧ___________________; БфаЮЮЊЗНГЬ
БфаЮЮЊЗНГЬ ЕФаЮЪН
ЕФаЮЪН