
【题目】如图,在△ABC中,CD⊥AB,且CD2=ADDB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DFDC.则下列结论正确的是( )
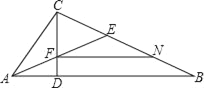
A. ①②④ B. ②③④ C. ①②③④ D. ①③
【答案】C
【解析】
根据已知条件可证△ADC∽△CDB,得出∠ACB=90°.根据等量关系及等腰三角形的性质得到CF=BN.根据同位角相等,证明FN∥AB.证明△ADF∽△CDA,根据相似三角形的性质得出AD2=DFDC.
①∵AE平分∠CAB,
∴∠CAE=∠DAF,
∴△CAE∽△DAF,
∴∠AFD=∠AEC,
∴∠CFE=∠AEC,
∴CF=CE,
∵CN=BE,
∴CE=BN,
∴CF=BN,故本选项正确;
②∵CD⊥AB,
∴∠ADC=∠CDB=90°,
∵CD2=ADDB,
∴![]() ,
,
∴△ADC∽△CDB,
∴∠ACD=∠B,
∴∠ACB=90°,故本选项正确;
③∵∠EAB=∠B,
∴EA=EB,
易知:∠ACF=∠ABC=∠EAB=∠EAC,
∴FA=FC,
易证:CF=CE,
∴CF=AF=CE,
∵FA=FC=BN,EA=EB,
∴EF=CE,
∴![]() ,
,
∵∠FEN=∠AEB,
∴△EFN∽△EAB,
∴∠EFN=∠EAB,
∴FN∥AB,故本选项正确;
④易证△ADF∽△CDA,
∴AD2=DFDC,故本选项正确;
故选:C.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
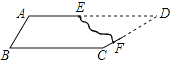
【题目】有一块形状如图所示的玻璃,不小心把DEF部分打碎,现在只测得AB=60cm,BC=80cm,∠A=120°,∠B=60°,∠C=150°,你能设计一个方案,根据测得的数据求出AD的长吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);

(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个不透明的袋子中装有7个只有颜色不同的球,其中2个白球,5个红球.
(1)求从袋中随机摸出一个球是红球的概率.
(2)从袋中随机摸出一个球,记录颜色后放回,摇匀,再随机摸出一个球,求两次摸出的球恰好颜色不同的概率.
(3)若从袋中取出若干个红球,换成相同数量的黄球.搅拌均匀后,使得随机从袋中摸出两个球,颜色是一白一黄的概率为![]() ,求袋中有几个红球被换成了黄球.
,求袋中有几个红球被换成了黄球.
查看答案和解析>>
科目:初中数学 来源: 题型:
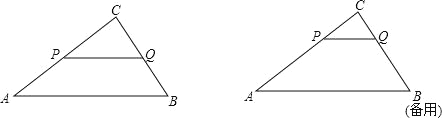
【题目】如图:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合),Q在BC上.
(1)当△PQC的面积与四边形PABQ的面积相等时,求CP的长;
(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长;
(3)试问:在AB上是否存在一点M,使得△PQM为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com