练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知点M(1-a，a+3)在第二象限，则a的取值范围是（   ）    

    A.a>-2        B. -2<a<1       C. a<-2        D. a>1


    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


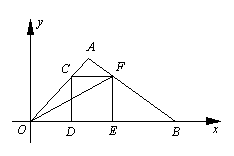
    在直角坐标系中，O为坐标原点，点A的坐标为（2，2），点C是线段OA上的一个动点（不运动至O，A两点），过点C作CD⊥x轴，垂足为D，以CD为边在右侧作正方形CDEF. 连接AF并延长交x轴的正半轴于点B，连接OF,设OD＝t.

    ⑴tan∠FOB=           ；

    ⑵ 已知二次函数图像 经过O、C、F三点，求二次函数的解析式；

    ⑶ 当t为何值时以B，E，F为顶点的三角形与△OFE相似．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读下列材料：求函数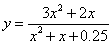的最大值.

    解：将原函数转化成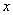的一元二次方程，得.

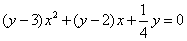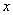    ∵为实数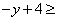，∴△＝＝0.

    ∴.因此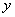，的最大值为4.

    根据材料给你的启示，求函数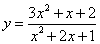的最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     一次函数y=ax+b与反比例函数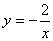,x与y的对应值如下表：

    x

    -3

    -2

    -1

    1

    2

    3

    y=ax+b

    4

    3

    2

    0

    -1

    -2

    1

    2

    -2

    -1

    方程ax+b=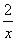－的解为___              __；不等式ax+b>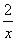－的解集为___         __.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    有四张形状、大小和质地相同的卡片A、B、C、D，正面分别写有一个正多边形（所有正多边形的边长相等），把四张卡片洗匀后正面朝下放在桌面上，从中随机抽取一张（不放回），接着再随机抽取一张．

    （1）请你用画树形图或列表的方法列举出可能出现的所有结果；

    （2）如果在（1）中各种结果被选中的可能性相同，求两次抽取的正多边形能构成平面镶嵌的概率；

    （3）若两种正多边形构成平面镶嵌，p、q表示这两种正多边形的个数，x、y表示对应正多边形的每个内角的度数，则有方程px+qy=360，求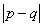的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示实数在数轴上的位置，以下四个命题中是假命题的是（   ）

    A.             B.

    C.                D.

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一组数据1，-1，0，-1，1的方差和标准差分别是             

    查看答案和解析>>

    科目：初中数学 来源： 题型：


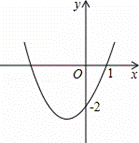
    如图，抛物线y=ax2+bx+c（a≠0）过点（1，0）和点（0，﹣2），且顶点在第三象限，设P=a﹣b+c，则P的取值范围是（　　）                 （2013中考题改编）

    　

    A．

    ﹣4＜P＜0

    B．

    ﹣4＜P＜﹣2

    C．

    ﹣2＜P＜0

    D．

    ﹣1＜P＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列算式中，正确的是（     ）

     A、  B、  C、

     D、

    查看答案和解析>>

    同步练习册答案