
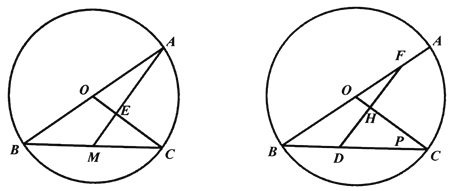
【题目】如图已知:AB是圆O的直径,AB=10,点C为圆O上异于点A、B的一点,点M为弦BC的中点.
(1)如果AM交OC于点E,求OE:CE的值;
(2)如果AM⊥OC于点E,求∠ABC的正弦值;
(3)如果AB:BC=5:4,D为BC上一动点,过D作DF⊥OC,交OC于点H,与射线BO交于圆内点F,请完成下列探究.
探究一:设BD=x,FO=y,求y关于x的函数解析式及其定义域.
探究二:如果点D在以O为圆心,OF为半径的圆上,写出此时BD的长度.
【答案】(1)OE:CE=1:2;(2)![]() ;(3)探究一:
;(3)探究一:![]() (其中
(其中![]() ),探究二:
),探究二:![]() .
.
【解析】
(1)过点O作ON║BC交AM于点N,根据AB是圆O的直径,点M为弦BC的中点即可;
(2)证明△OME∽△MCE,求出![]() 即可;
即可;
(3)过点D作DL⊥BO于点L,设BD=![]() ,则CD=
,则CD=![]() ,BL=DL=
,BL=DL=![]() ,CH=
,CH=![]() ,OH=
,OH= ![]() ,根据
,根据![]() ,求出y的解析式,再根据OC垂直平分DF,求出BD即可.
,求出y的解析式,再根据OC垂直平分DF,求出BD即可.
解:(1)过点O作ON║BC交AM于点N,
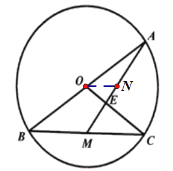
∵AB是圆O的直径,ON∥BM,∴![]()
∵点M为弦BC的中点,∴ ![]()
∴OE:CE=ON:BM=1:2
(2)∵点M为弦BC的中点,
∴OM⊥BC.
∴∠C+∠MOC=90°,
∵AM⊥OC于点E,
∴∠MOC+∠OME=90°,
∴∠OME=∠C.
∵∠OME=∠C,∠MOE=∠MOE,
∴△OME∽△MCE
∴![]() .
.
设OE=![]() ,则CE=2
,则CE=2![]() , ME=
, ME=![]()
在直角△MCE中,![]() ,
,![]()
∴![]() .
.
(3)过点D作DL⊥BO于点L,
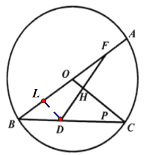
∵AB=10,AB:BC=5:4,
∴BC=8,
设BD=![]() ,则CD=
,则CD=![]() ,BL=DL=
,BL=DL=![]() ,CH=
,CH=![]() ,OH=
,OH= ![]() ,
,
∵OH∥LD,
∴![]()
∴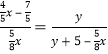
∴![]() (其中
(其中![]() )
)
∵以O为圆心,OF为半径的圆经过D,
∴OC垂直平分DF,FO=OL,
![]()
![]() ,
,
![]()
此时.
![]()


科目:初中数学 来源: 题型:
【题目】某地发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A,B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD,点E在边AD上,AF⊥BE,垂足为点F,点G在线段BF上,BG=AF.
(1)求证:CG⊥BE;
(2)如果点E是AD的中点,联结CF,求证:CF=CB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲜丰水果店计划用![]() 元/盒的进价购进一款水果礼盒以备销售.
元/盒的进价购进一款水果礼盒以备销售.
![]() 据调查,当该种水果礼盒的售价为
据调查,当该种水果礼盒的售价为![]() 元/盒时,月销量为
元/盒时,月销量为![]() 盒,每盒售价每增长
盒,每盒售价每增长![]() 元,月销量就相应减少
元,月销量就相应减少![]() 盒,若使水果礼盒的月销量不低于
盒,若使水果礼盒的月销量不低于![]() 盒,每盒售价应不高于多少元?
盒,每盒售价应不高于多少元?
![]() 在实际销售时,由于天气和运输的原因,每盒水果礼盒的进价提高了
在实际销售时,由于天气和运输的原因,每盒水果礼盒的进价提高了![]() ,而每盒水果礼盒的售价比(1)中最高售价减少了
,而每盒水果礼盒的售价比(1)中最高售价减少了![]() ,月销量比(1)中最低月销量
,月销量比(1)中最低月销量![]() 盒增加了
盒增加了![]() ,结果该月水果店销售该水果礼盒的利润达到了
,结果该月水果店销售该水果礼盒的利润达到了![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长_____.
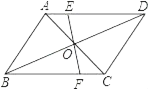
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于C点,其中
轴交于C点,其中![]() .
.
(1)求点B的坐标及此抛物线的表达式;
(2)点D为y轴上一点,若直线BD和直线BC的夹角为15,求线段CD的长度;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,当
上的一个动点,当![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.
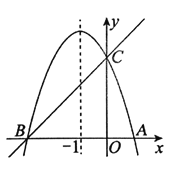
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
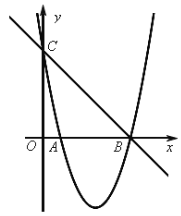
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用8个大小相同的小正方体搭成的几何体,仅在该几何体中取走一块小正方体,使得到的新几何体同时满足两个要求:(1)从正面看到的形状和原几何体从正面看到的形状相同;(2)从左面看到的形状和原几何体从左面看到的形状也相同.在不改变其它小正方体位置的前提下,可取走的小正方体的标号是_____.
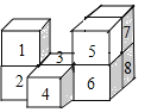
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com