
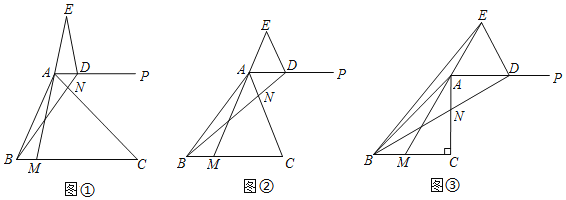
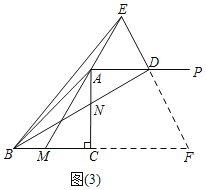
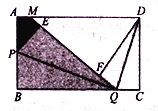
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬CA£½CB£¬0”ć£¼”ĻC”Ü90”ć£®¹żµćA×÷ÉäĻßAP”ĪBC£¬µćM”¢N·Ö±šŌŚ±ßBC”¢ACÉĻ£ØµćM”¢N²»ÓėĖłŌŚĻ߶Ī¶ĖµćÖŲŗĻ£©£¬ĒŅBM£½AN£¬Į¬½įBN²¢ŃÓ³¤½»APÓŚµćD£¬Į¬½įMA²¢ŃÓ³¤½»ADµÄ“¹Ö±Ę½·ÖĻßÓŚµćE£¬Į¬½įED£®
£Ø²ĀĻė£©ČēĶ¼¢Ł£¬µ±”ĻC£½45”揱£¬æÉÖ¤”÷BCN”Õ”÷ACM£¬“Ó¶ųµĆ³ö”ĻCBN£½”ĻCAM£¬½ų¶ųµĆ³ö”ĻBDEµÄ“óŠ”ĪŖ”” ””¶Č£®
£ØĢ½¾æ£©ČēĶ¼¢Ś£¬Čō”ĻC£½¦Į£®
£Ø1£©ĒóÖ¤£ŗ”÷BCN”Õ”÷ACM£®
£Ø2£©”ĻBDEµÄ“óŠ”ĪŖ”” ””¶Č£ØÓĆŗ¬aµÄ“śŹżŹ½±ķŹ¾£©£®
£ØÓ¦ÓĆ£©ČēĶ¼¢Ū£¬µ±”ĻC£½90”揱£¬Į¬½įBE£®ČōBC£½3£¬”ĻBAM£½15”ć£¬Ōņ”÷BDEµÄĆ껿ĪŖ”” ””£®
”¾“š°ø”放²ĀĻė”æ135”ć£»”¾Ģ½¾æ”æ£Ø1£©Ļź¼ū½āĪö£»£Ø2£©¦Į»ņ£Ø180©¦Į£©£»”¾Ó¦ÓĆ”æ9![]() ©9£®
©9£®
”¾½āĪö”æ
²ĀĻė£ŗČēĶ¼£Ø1£©ÖŠ£¬ŃÓ³¤ED½»BCÓŚµćF£¬½»ACÓŚµćO£®Ļė°ģ·ØÖ¤Ć÷”ĻBNC£½”ĻBFE£¬ŌŁĄūÓĆČż½ĒŠĪµÄĶā½ĒµÄŠŌÖŹ¼“æɽā¾öĪŹĢā£»
Ģ½¾æ£ŗ£Ø1£©Ķ¬Ąķøł¾ŻSASÖ¤Ć÷£ŗ”÷BCN”Õ”÷ACM£»
£Ø2£©·ÖĮ½ÖÖĒéŠĪĢÖĀŪĒó½ā¼“æÉ£¬¢ŁČēĶ¼2ÖŠ£¬µ±µćEŌŚAMµÄŃÓ³¤ĻßÉĻŹ±£¬¢ŚČēĶ¼4ÖŠ£¬µ±µćEŌŚMAµÄŃÓ³¤ĻßÉĻŹ±£¬·Ö±š¼ĘĖć¼“æÉ£»
Ó¦ÓĆ£ŗČēĶ¼3£¬·Ö±š¼ĘĖćBDŗĶDEµÄ³¤£¬Ö¤Ć÷”÷EADŹĒµČ±ßČż½ĒŠĪ£¬øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½æÉµĆ½įĀŪ£®
²ĀĻė£ŗÖ¤Ć÷£ŗČēĶ¼1ÖŠ£¬ŃÓ³¤ED½»BCÓŚµćF£¬½»ACÓŚµćO£¬
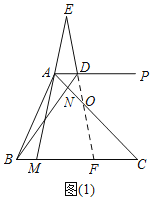
”ßCB£½CA£¬
”ą”ĻABM£½”ĻBAN£¬
”ßCA£½CB£¬BM£½AN£¬
”ąCM£½CN£¬
”ß”ĻC£½”ĻC£¬
”ą”÷BCN”Õ”÷ACM£ØSAS£©£¬
”ą”ĻCBN£½”ĻCAM£¬
”ßEŹĒADµÄ“¹Ö±Ę½·ÖĻßÉĻµÄµć£¬
”ąEA£½ED£¬
”ą”ĻEAD£½”ĻEDA£¬
”ßAD”ĪBC£¬
”ą”ĻEAD£½”ĻEMF£¬”ĻEDA£½”ĻEFM£¬
”ą”ĻBNC£½”ĻBFE£¬
”ą”ĻNOD+”ĻBDF£½”ĻC+”ĻFOC£¬
”ß”ĻC£½45”ć£¬”ĻFOC£½”ĻNOD£¬
”ą”ĻNDO£½45”ć£¬
”ą”ĻBDE£½135”ć£¬
¹Ź“š°øĪŖ£ŗ135”ć£»
Ģ½¾æ£ŗ
£Ø1£©Ö¤Ć÷£ŗ”ßCA£½CB£¬BM£½AN£¬
”ąCA©AN£½CB©BM£¬
”ąMC£½NC£¬
Ó֔ߔĻC£½”ĻC£¬
”ą”÷BCN”Õ”÷ACM£ØSAS£©£»
£Ø2£©·ÖĮ½ÖÖĒéæö£ŗ
¢ŁČēĶ¼2ÖŠ£¬µ±µćEŌŚAMµÄŃÓ³¤ĻßÉĻŹ±£¬
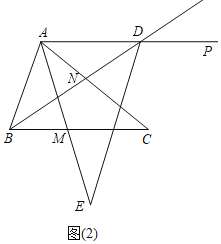
Ņ×Ö¤£ŗ”ĻCBN£½”ĻADB£½”ĻCAN£¬”ĻACB£½”ĻCAD£¬
”ßEA£½ED£¬
”ą”ĻEAD£½”ĻEDA£¬
”ą”ĻCAM+”ĻCAD£½”ĻBDE+”ĻADB£¬
”ą”ĻBDE£½”ĻCAD£½”ĻACB£½¦Į£®
ČēĶ¼4ÖŠ£¬µ±µćEŌŚMAµÄŃÓ³¤ĻßÉĻŹ±£¬ŃÓ³¤ED½»BCµÄŃÓ³¤ĻßÓŚµćF£¬
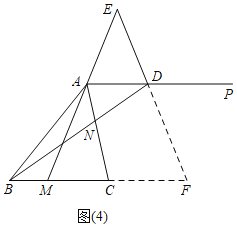
Ķ¬ĄķµĆ”÷BCN”Õ”÷ACM£ØSAS£©£¬
”ą”ĻCBN£½”ĻCAM£¬
Ķ¬ĄķµĆ£ŗ”ĻBNC£½”ĻAMC£½”ĻBFE£¬
”ą”ĻBNC+”ĻNBC£½”ĻNBC+”ĻBFE£¬
”ą”ĻACB£½”ĻBDF£½¦Į£¬
”ą”ĻBDE£½180”橦Į£®
¹Ź“š°øĪŖ£ŗ¦Į»ņ£Ø180©¦Į£©£»
Ó¦ÓĆ£ŗ
ČēĶ¼3£¬Ķ¬£Ø2£©µĆ£ŗ”ĻBDE£½180”ć©”ĻACB£½90”ć£¬
”ß”ĻACB£½90”ć£¬AC£½BC£½3£¬
”ą”ĻBAC£½”ĻABC£½45”ć£¬
”ß”ĻBAM£½15”ć£¬
”ą”ĻCAM£½”ĻCBN£½30”ć£¬
Rt”÷BNCÖŠ£¬CN£½![]() £¬BN£½
£¬BN£½![]() £¬
£¬
”ąAN£½AC©CN£½3©![]() £¬
£¬
”ßAD”ĪBC£¬
”ą”ĻDAN£½”ĻACB£½90”ć£¬”ĻADN£½”ĻNBC£½30”ć£¬
”ąDN£½2AN£½6©2![]() £¬AD£½
£¬AD£½![]() AN£½3
AN£½3![]() ©3£¬
©3£¬
”ąBD£½BN+DN£½2![]() +6©2
+6©2![]() £½6£¬
£½6£¬
”ßEA£½ED£¬”ĻEAD£½60”ć£¬
”ą”÷EADŹĒµČ±ßČż½ĒŠĪ£¬
”ąED£½AD£½3![]() ©3£¬
©3£¬
”ąS”÷BDE£½![]()
¹Ź“š°øĪŖ£ŗ9![]() ©9£®
©9£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĄķ½ā£ŗ¶ŌÓŚČĪŅāÕżŹµŹża”¢b£¬”ß![]() ”Ż0£¬”””ą
”Ż0£¬”””ą![]() ”Ż0£¬
”Ż0£¬
”ą![]() ”Ż
”Ż![]() £¬Ö»ÓŠµ±a£½bŹ±£¬µČŗųÉĮ¢£®
£¬Ö»ÓŠµ±a£½bŹ±£¬µČŗųÉĮ¢£®
½įĀŪ£ŗŌŚ![]() ”Ż
”Ż![]() £Øa”¢b¾łĪŖÕżŹµŹż£©ÖŠ£¬ČōabĪŖ¶ØÖµp£¬Ōņa+b”Ż
£Øa”¢b¾łĪŖÕżŹµŹż£©ÖŠ£¬ČōabĪŖ¶ØÖµp£¬Ōņa+b”Ż![]() £¬Ö»ÓŠµ±a£½bŹ±£¬a+bÓŠ×īŠ”Öµ
£¬Ö»ÓŠµ±a£½bŹ±£¬a+bÓŠ×īŠ”Öµ![]() £®
£®
øł¾ŻÉĻŹöÄŚČŻ£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
Čōm£¾0£¬Ö»ÓŠµ±m£½ Ź±£¬![]() ÓŠ×īŠ”Öµ £®
ÓŠ×īŠ”Öµ £®
Ė¼æ¼ŃéÖ¤£ŗČēĶ¼1£¬ABĪŖ°ėŌ²OµÄÖ±¾¶£¬CĪŖ°ėŌ²ÉĻČĪŅāŅ»µć£ØÓėµćA”¢B²»ÖŲŗĻ£©£¬¹żµćC×÷CD”ĶAB£¬“¹×ćĪŖD£¬AD£½a£¬DB£½b£®
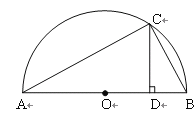
ŹŌøł¾ŻĶ¼ŠĪŃéÖ¤![]() ”Ż
”Ż![]() £¬²¢Öø³öµČŗųÉĮ¢Ź±µÄĢõ¼ž£®
£¬²¢Öø³öµČŗųÉĮ¢Ź±µÄĢõ¼ž£®
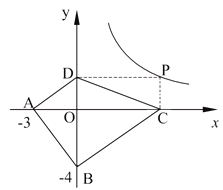
Ģ½Ė÷Ó¦ÓĆ£ŗČēĶ¼2£¬ŅŃÖŖA(£3£¬0)£¬B(0£¬£4)£¬PĪŖĖ«ĒśĻß![]() £Øx£¾0£©ÉĻµÄČĪŅāŅ»µć£¬¹żµćP×÷PC”ĶxÖįÓŚµćC£¬PD”ĶyÖįÓŚµćD£®ĒóĖıߊĪABCDĆ껿µÄ×īŠ”Öµ£¬²¢ĖµĆ÷“ĖŹ±ĖıߊĪABCDµÄŠĪד£®
£Øx£¾0£©ÉĻµÄČĪŅāŅ»µć£¬¹żµćP×÷PC”ĶxÖįÓŚµćC£¬PD”ĶyÖįÓŚµćD£®ĒóĖıߊĪABCDĆ껿µÄ×īŠ”Öµ£¬²¢ĖµĆ÷“ĖŹ±ĖıߊĪABCDµÄŠĪד£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() ÖŠ£¬
ÖŠ£¬![]() £¬µć
£¬µć![]() ”¢
”¢![]() Ķ¬Ź±“Óµć
Ķ¬Ź±“Óµć![]() ³ö·¢£¬ŅŌ
³ö·¢£¬ŅŌ![]() µÄĖŁ¶Č·Ö±šŃŲ
µÄĖŁ¶Č·Ö±šŃŲ![]() ”¢
”¢![]() ŌČĖŁŌĖ¶Æ£¬µ±µć
ŌČĖŁŌĖ¶Æ£¬µ±µć![]() µ½“ļµć
µ½“ļµć![]() Ź±£¬Į½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖ
Ź±£¬Į½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖ![]() £®¹żµć
£®¹żµć![]() ×÷
×÷![]() µÄ“¹Ļß
µÄ“¹Ļß![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬µć
£¬µć![]() Óėµć
Óėµć![]() ¹ŲÓŚÖ±Ļß
¹ŲÓŚÖ±Ļß![]() ¶Ō³Ę£®
¶Ō³Ę£®
£Ø1£©µ±![]() _____
_____![]() Ź±£¬µć
Ź±£¬µć![]() ŌŚ
ŌŚ![]() µÄĘ½·ÖĻßÉĻ£»
µÄĘ½·ÖĻßÉĻ£»
£Ø2£©µ±![]() _____
_____![]() Ź±£¬µć
Ź±£¬µć![]() ŌŚ
ŌŚ![]() ±ßÉĻ£»
±ßÉĻ£»
£Ø3£©Éč![]() Óė
Óė![]() ÖŲŗĻ²æ·ÖµÄĆ껿ĪŖ
ÖŲŗĻ²æ·ÖµÄĆ껿ĪŖ![]() £¬Ēó
£¬Ēó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
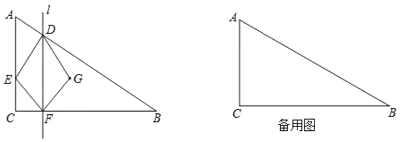
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪÖ½Ę¬![]() £¬
£¬![]() ŹĒ
ŹĒ![]() µÄÖŠµć£¬
µÄÖŠµć£¬![]() ŹĒ
ŹĒ![]() ÉĻŅ»¶Æµć£¬
ÉĻŅ»¶Æµć£¬![]() ŃŲ
ŃŲ![]() ÕŪµž£¬µć
ÕŪµž£¬µć![]() ĀäŌŚµć
ĀäŌŚµć![]() “¦£»ŃÓ³¤
“¦£»ŃÓ³¤![]() ½»
½»![]() ÓŚ
ÓŚ![]() µć£¬Į¬½Ó
µć£¬Į¬½Ó![]() .
.
£Ø1£©ĒóÖ¤£ŗ![]() ”Õ
”Õ![]() £»
£»
£Ø2£©µ±![]() Ź±£¬½«
Ź±£¬½«![]() ŃŲ
ŃŲ![]() ÕŪµž£¬µć
ÕŪµž£¬µć![]() ĀäŌŚĻ߶Ī
ĀäŌŚĻ߶Ī![]() ÉĻµć
ÉĻµć![]() “¦.
“¦.
¢ŁĒóÖ¤£ŗ![]() ”×
”×![]() £»
£»
¢ŚČē¹ū![]() £¬
£¬![]() £¬Ēó
£¬Ēó![]() µÄ³¤.
µÄ³¤.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
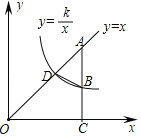
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy£½xÓė·“±ČĄżŗÆŹży£½![]() £Øx£¾0£©µÄĶ¼ĻóĻą½»ÓŚµćD£¬µćAĪŖÖ±Ļßy£½xÉĻŅ»µć£¬¹żµćA×÷AC”ĶxÖįÓŚµćC£¬½»·“±ČĄżŗÆŹży£½
£Øx£¾0£©µÄĶ¼ĻóĻą½»ÓŚµćD£¬µćAĪŖÖ±Ļßy£½xÉĻŅ»µć£¬¹żµćA×÷AC”ĶxÖįÓŚµćC£¬½»·“±ČĄżŗÆŹży£½![]() £Øx£¾0£©µÄĶ¼ĻóÓŚµćB£¬Į¬½ÓBD£®
£Øx£¾0£©µÄĶ¼ĻóÓŚµćB£¬Į¬½ÓBD£®
£Ø1£©ČōµćBµÄ×ų±źĪŖ£Ø8£¬2£©£¬Ōņk£½”” ””£¬µćDµÄ×ų±źĪŖ”” ””£»
£Ø2£©ČōAB£½2BC£¬ĒŅ”÷OACµÄĆ껿ĪŖ18£¬ĒókµÄÖµ¼°”÷ABDµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ»ĘŹÆŹŠŌŚ““½Ø¹ś¼Ņ¼¶ĪÄĆ÷ĪĄÉś³ĒŹŠÖŠ£¬ĀĢ»Æµµ“Ī²»¶ĻĢįÉż£®Ä³Š£¼Ę»®¹ŗ½ųA£¬BĮ½ÖÖŹ÷ľ¹²100æĆ½ųŠŠŠ£Ō°ĀĢ»ÆÉż¼¶£¬¾ŹŠ³”µ÷²é£ŗ¹ŗĀņAÖÖŹ÷ľ2æĆ£¬BÖÖŹ÷ľ5æĆ£¬¹²Šč600ŌŖ£»¹ŗĀņAÖÖŹ÷ľ3æĆ£¬BÖÖŹ÷ľ1æĆ£¬¹²Šč380ŌŖ£®
£Ø1£©ĒóAÖÖ£¬BÖÖŹ÷ľĆææĆø÷¶ąÉŁŌŖ£æ
£Ø2£©Ņņ²¼¾ÖŠčŅŖ£¬¹ŗĀņAÖÖŹ÷ľµÄŹżĮæ²»ÉŁÓŚBÖÖŹ÷ľŹżĮæµÄ3±¶£®Ń§Š£ÓėÖŠ±ź¹«Ė¾Ē©¶©µÄŗĻĶ¬ÖŠ¹ę¶Ø£ŗŌŚŹŠ³”¼Ūøń²»±äµÄĒéæöĻĀ£Ø²»æ¼ĀĒĘäĖūŅņĖŲ£©£¬Źµ¼Źø¶æī×ܽš¶ī°“ŹŠ³”¼Ū¾ÅÕŪÓÅ»Ż£¬ĒėÉč¼ĘŅ»ÖÖ¹ŗĀņŹ÷ľµÄ·½°ø£¬Ź¹Źµ¼ŹĖł»Ø·ŃÓĆ×īŹ”£¬²¢Ēó³ö×īŹ”µÄ·ŃÓĆ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗŌŚ![]() ÖŠ£¬ŅŌ
ÖŠ£¬ŅŌ![]() ±ßĪŖÖ±¾¶µÄ
±ßĪŖÖ±¾¶µÄ![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬ŌŚĮÓ»”
£¬ŌŚĮÓ»”![]() ÉĻČ”Ņ»µć
ÉĻČ”Ņ»µć![]() Ź¹
Ź¹![]() £¬ŃÓ³¤
£¬ŃÓ³¤![]() ŅĄ“Ī½»
ŅĄ“Ī½»![]() ÓŚµć
ÓŚµć![]() £¬½»
£¬½»![]() ÓŚ
ÓŚ![]() £®
£®
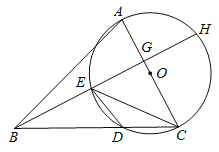
£Ø1£©ĒóÖ¤£ŗ![]() £»
£»
£Ø2£©Čō![]() £¬
£¬![]() µÄÖ±¾¶µČÓŚ10£¬
µÄÖ±¾¶µČÓŚ10£¬![]() £¬Ēó
£¬Ēó![]() µÄ³¤£®
µÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ½ā±¾Š£¾ÅÄź¼¶Ń§ÉśĘŚÄ©ŹżŃ§æ¼ŹŌĒéæö£¬Š”ĮĮŌŚ¾ÅÄź¼¶Ė껜³éČ”ĮĖŅ»²æ·ÖѧɜµÄĘŚÄ©ŹżŃ§³É¼ØĪŖŃł±¾£¬·ÖĪŖ![]() ·Ö)”¢
·Ö)”¢![]() ·Ö)”¢
·Ö)”¢![]() ·Ö)”¢
·Ö)”¢![]() ·Ö)ĖÄøöµČ¼¶½ųŠŠĶ³¼Ę£¬²¢½«Ķ³¼Ę½į¹ū»ęÖĘ³ÉČēĻĀĶ³¼ĘĶ¼±ķ£¬ĒėÄćøł¾ŻĶ³¼ĘĶ¼½ā“šŅŌĻĀĪŹĢā£ŗ
·Ö)ĖÄøöµČ¼¶½ųŠŠĶ³¼Ę£¬²¢½«Ķ³¼Ę½į¹ū»ęÖĘ³ÉČēĻĀĶ³¼ĘĶ¼±ķ£¬ĒėÄćøł¾ŻĶ³¼ĘĶ¼½ā“šŅŌĻĀĪŹĢā£ŗ
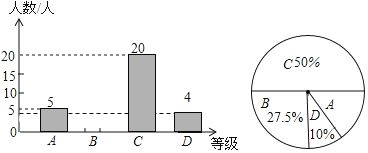
ĘäÖŠ×é![]() µÄĘŚÄ©ŹżŃ§³É¼ØČēĻĀ
µÄĘŚÄ©ŹżŃ§³É¼ØČēĻĀ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
£Ø1£©Ēė²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø2£©Õā²æ·ÖѧɜµÄĘŚÄ©ŹżŃ§³É¼ØµÄÖŠĪ»ŹżŹĒ £¬![]() ×éµÄĘŚÄ©ŹżŃ§³É¼ØµÄÖŚŹżŹĒ £»
×éµÄĘŚÄ©ŹżŃ§³É¼ØµÄÖŚŹżŹĒ £»
£Ø3£©ÕāøöѧŠ£¾ÅÄź¼¶¹²ÓŠŃ§Éś![]() ČĖ£¬Čō·ÖŹżĪŖ
ČĖ£¬Čō·ÖŹżĪŖ![]() ·Ö(ŗ¬
·Ö(ŗ¬![]() ·Ö)ŅŌÉĻĪŖÓÅŠć£¬Ēė¹Ą¼ĘÕā“Ī¾ÅÄź¼¶Ń§ÉśĘŚÄ©ŹżŃ§æ¼ŹŌ³É¼ØĪŖÓÅŠćµÄѧɜČĖŹż“óŌ¼ÓŠ¶ąÉŁ£æ
·Ö)ŅŌÉĻĪŖÓÅŠć£¬Ēė¹Ą¼ĘÕā“Ī¾ÅÄź¼¶Ń§ÉśĘŚÄ©ŹżŃ§æ¼ŹŌ³É¼ØĪŖÓÅŠćµÄѧɜČĖŹż“óŌ¼ÓŠ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°½ńÓŠÉĘŠŠÕߊŠŅ»°Ł²½£¬²»ÉĘŠŠÕߊŠĮłŹ®²½”±£Ø³ö×Ō”¶¾ÅÕĀĖćŹõ”·£©ŅāĖ¼ŹĒ£ŗĶ¬ŃłŹ±¼ä¶ĪÄŚ£¬×ßĀ·æģµÄČĖÄÜ×ß100²½£¬×ßĀ·ĀżµÄČĖÖ»ÄÜ×ß60²½£¬¼Ł¶ØĮ½Õß²½³¤ĻąµČ£¬¾Ż“Ė»Ų“šŅŌĻĀĪŹĢā£ŗ
£Ø1£©½ń²»ÉĘŠŠÕßĻČŠŠŅ»°Ł²½£¬ÉĘŠŠÕß×·Ö®£¬²»ÉĘŠŠÕßŌŁŠŠĮł°Ł²½£¬ĪŹŹėÖĮÓŚĒ°£¬Į½Õß¼øŗĪ²½øōÖ®£æ¼“£ŗ×ßĀ·ĀżµÄČĖĻČ×ß100²½£¬×ßĀ·æģµÄČĖæŖŹ¼×·øĻ£¬µ±×ßĀ·ĀżµÄČĖŌŁ×ß600²½Ź±£¬ĒėĪŹĖŌŚĒ°Ćę£¬Į½ČĖĻąøō¶ąÉŁ²½£æ
£Ø2£©½ń²»ÉĘŠŠÕßĻČŠŠĮ½°Ł²½£¬ÉĘŠŠÕß×·Ö®£¬ĪŹ¼øŗĪ²½¼°Ö®£æ¼“£ŗ×ßĀ·ĀżµÄČĖĻČ×ß200²½£¬ĒėĪŹ×ßĀ·æģµÄČĖ×߶ąÉŁ²½²ÅÄÜ×·ÉĻ×ßĀ·ĀżµÄČĖ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com