
【题目】如图, ![]() 中,
中, ![]() ,
,![]() ,
, ![]() 的平分线与
的平分线与![]() 的垂直平分线交于点
的垂直平分线交于点![]() ,将
,将![]() 沿
沿![]() (
(![]() 在
在![]() 上,
上, ![]() 在
在![]() 上)折叠,点
上)折叠,点![]() 与点
与点![]() 恰好重合,则
恰好重合,则![]() 的度数是( )
的度数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
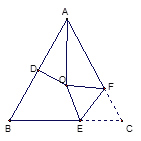
【解析】试题分析:如图,连接OB、OC,
∵∠BAC=54°,AO为∠BAC的平分线,
∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×54°=27°,
×54°=27°,
又∵AB=AC,
∴∠ABC=![]() (180°-∠BAC)=
(180°-∠BAC)= ![]() (180°-54°)=63°,
(180°-54°)=63°,
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=27°,
∴∠OBC=∠ABC-∠ABO=63°-27°=36°,
∵AO为∠BAC的平分线,AB=AC,
∴OB=OC,
∴点O在BC的垂直平分线上,
又∵DO是AB的垂直平分线,
∴点O是△ABC的外心,
∴∠OCB=∠OBC=36°,
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE,
∴∠COE=∠OCB=36°,
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°,
故选:B.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=﹣1,给出下列结论:(1)b2>4ac; (2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.其中正确的结论有( )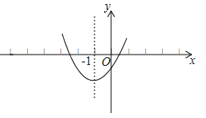
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的直径,DA、DC分别是⊙O的切线,点A、C是切点,连接DO交弧AC于点E,连接AE、CE.
(1)如图1,求证:EA=EC;
(2)如图2,延长DO交⊙O于点F,连接CF、BE交于点G,求证:∠CGE=2∠F;
(3)如图3,在(2)的条件下,DE=![]() AD,EF=2
AD,EF=2![]() , 求线段CG的长.
, 求线段CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在反比例函数y=![]() (x<0)的图象上,AD∥x轴,AB∥y轴,点B在反比例函数y=
(x<0)的图象上,AD∥x轴,AB∥y轴,点B在反比例函数y=![]() (x<0)的图象上,过点B作BC∥x轴,交y轴于点C,若四边形ABCD的面积为8,则k的值为
(x<0)的图象上,过点B作BC∥x轴,交y轴于点C,若四边形ABCD的面积为8,则k的值为 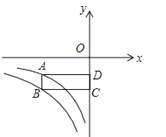
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离,即|x|=|x﹣0|,也就是说|x|表示在数轴上数x与数0对应点之间的距离;这个结论可以推广为:|x﹣y|表示在数轴上数x、y对应点之间的距离;在解题中,我们常常运用绝对值的几何意义.
①解方程|x|=2,容易看出,在数轴上与原点距离为2的点对应的数为±2,即该方程的解为x=±2.
②在方程|x﹣1|=2中,x的值就是数轴上到1的距离为2的点对应的数,显然x=3或x=﹣1.
③在方程|x﹣1|+|x+2|=5中,显然该方程表示数轴上与1和﹣2的距离之和为5 的点对应的x值,在数轴上1和﹣2的距离为3,满足方程的x的对应点在1的右边或﹣2的左边.若x的对应点在1的右边,由图示可知,x=2;同理,若x的对应点在﹣2的左边,可得x=﹣3,所以原方程的解是x=2或x=﹣3.根据上面的阅读材料,解答下列问题:
(1)方程|x|=5的解是_______________.
(2)方程|x﹣2|=3的解是_________________.
(3)画出图示,解方程|x﹣3|+|x+2|=9.

查看答案和解析>>
科目:初中数学 来源: 题型:
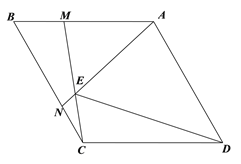
【题目】如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.
(1)证明△BCM≌△CAN;
(2)∠AEM= °;
(3)求证DE平分∠AEC;
(4)试猜想AE,CE,DE之间的数量关系并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com