�ڢۢܢ�
���������ݷ�����������ͼ������ʣ��ر��Ǹ��ݷ���������k�ļ������壬�Ը�С����һ���з��������ɵó���ȷ�𰸣�
��𣺸������⣬��P���A�ĺ�������ͬ�����Ǹ�������P����������ڵ�A�������꣬
��

��-

��
���k��-1��
��ٴ�����ȷ��
��y=-

��
��S
��ODB=

��|x|•|y|=

��
S
��OCA=

��|x|•|y|=

��
��S
��ODB=S
��OCA���ʢ���ȷ��
�ߵ�P��y=

�ϣ�
��S
����PCOD=|x|•|y|=|k|��
��S
�ı���PAOB=S
����PCOD-S
��ODB-S
��OCA=|k|-

-

=-k-1��
���ı���PAOB��������ᷢ���仯���ʢ���ȷ��
���P�������ǣ�a��

�������A�������ǣ�a��-

����
��PA=

-��-

��=

+

��
�ߵ�B��������Ϊ

��
��-

=

��
���x=-
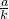
��
���B�������-
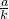
��
��PB=-
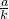
-a��
��PA=PB����

+

=-
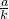
-a��
������

=-a��
�൱�ҽ�����P�ĺ�������������ij������ʱ��
���ı���PCOD���������ǣ�PA=PB���ʢݴ���
�ߵ�B��PD���е㣬
��a=2��-
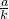
����
��k=-2��
�ֵ�P����������

����-

����A��������-

��
��-

=2��-

����
���Aһ����PC���е㣬�ʢ���ȷ��
����������һ����ȷ���Ǣڢۢܢޣ�
�ʴ�Ϊ���ڢۢܢޣ�
���������⿼�鷴�����������ۺ����ã��ۺ��Խ�ǿ���ؼ���֪������ͼ���ϵĵ�������ṹ�ɵ������ε�������ı��ε������k�Ĺ�ϵ��

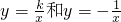 ���ڵڶ������ڵ�ͼ����ͼ��ʾ����P��
���ڵڶ������ڵ�ͼ����ͼ��ʾ����P�� ��ͼ���ϣ�PC��x
��ͼ���ϣ�PC��x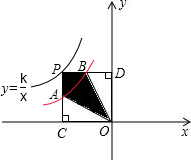 ���ڵ�C��
���ڵ�C��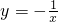 ��ͼ���ڵ�A��PD��y���ڵ�D��
��ͼ���ڵ�A��PD��y���ڵ�D��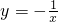 ��ͼ���ڵ�B������P��
��ͼ���ڵ�B������P�� ��ͼ�����˶�ʱ�����½��ۣ�
��ͼ�����˶�ʱ�����½��ۣ� ��-
��- ��
�� ��
�� ��|x|•|y|=
��|x|•|y|= ��
�� ��|x|•|y|=
��|x|•|y|= ��
�� �ϣ�
�ϣ� -
- =-k-1��
=-k-1�� �������A�������ǣ�a��-
�������A�������ǣ�a��- ����
���� -��-
-��- ��=
��= +
+ ��
�� ��
�� =
= ��
��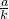 ��
��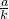 ��
��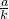 -a��
-a�� +
+ =-
=-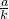 -a��
-a�� =-a��
=-a��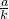 ����
���� ����-
����- ����A��������-
����A��������- ��
�� =2��-
=2��- ����
����

 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
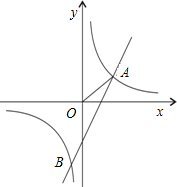 ��ͼ����֪����������y=
��ͼ����֪����������y=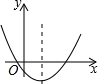 ���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����������y=
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����������y=