
【题目】在Rt△ABC中,AB=6,BC=8,则这个三角形的内切圆的半径是( )
A.5B.2C.5或2D.2或![]() -1
-1
【答案】D
【解析】
分AC为斜边和BC为斜边两种情况讨论.根据切线定理得过切点的半径垂直于三角形各边,利用面积法列式求半径长.
第一情况:当AC为斜边时,
如图,设⊙O是Rt△ABC的内切圆,切点分别为D,E,F,连接OC,OA,OB,
∴OD⊥AC, OE⊥BC,OF⊥AB,且OD=OE=OF=r,
在Rt△ABC中,AB=6,BC=8,由勾股定理得,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴r=2.

第二情况:当BC为斜边时,
如图,设⊙O是Rt△ABC的内切圆,切点分别为D,E,F,连接OC,OA,OB,
∴OD⊥BC, OE⊥AC,OF⊥AB,且OD=OE=OF=r,
在Rt△ABC中,AB=6,BC=8,由勾股定理得,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴r=![]() .
.

故选:D.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别相交于点B,C,连接AC.
(m≠0)的图象有公共点A(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别相交于点B,C,连接AC.

(1)求k和m的值;
(2)求点B的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
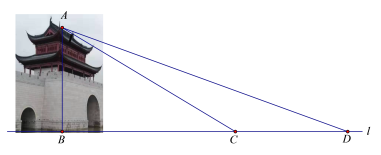
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
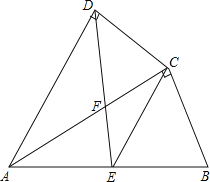
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,过点B、点C分别作BE∥CD,CE∥BD.
(1)求证:四边形BECD是菱形;
(2)若∠A=60°,AC=![]() ,求菱形BECD的面积.
,求菱形BECD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
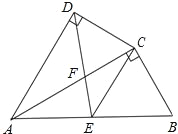
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:△AFD∽△CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月26日,鲁南高铁正式开通运营.鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿AC方向挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D共线)处同时施工.测得∠CAB=30°,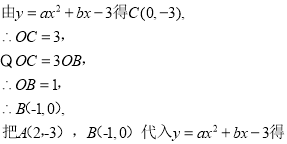 ,∠ABD=105°,求AD的长.
,∠ABD=105°,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣2x2+bx+c的图象经过点(0,6)和(1,8).
(1)求这个二次函数的解析式;
(2)①当x在什么范围内时,y随x的增大而增大?
②当x在什么范围内时,y>0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点,与y轴交于点C,对称轴为x=1.
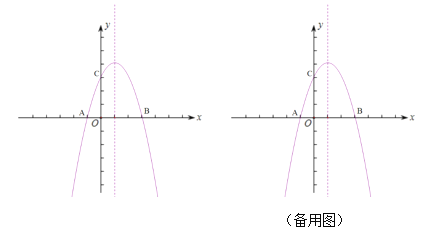
(1)求抛物线的函数表达式;
(2)在抛物线的对称轴上求一点P,使点P到点A的距离与到点C的距离之和最小,并求出此时点P的坐标;
(3)是否存在过A,B两点的抛物线,其顶点M关于x轴的对称点为N,使得四边形AMBN为正方形?若存在,请直接写出此抛物线的函数表达式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com