

| 2 |
| 3 |
| 5 |
| 6 |
| 6002+3002 |
| 5 |
| 5 |
| 300 |
| sin45° |
| 2 |
| 2 |
| EP |
| AP |
| E′P′ |
| AP′ |
| AP |
| 2 |
| AP′ |
| 2 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
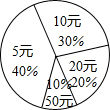 (2011•资阳)在资阳市团委发起的“暖冬行动”中,某班50名同学响应号召,纷纷捐出零花钱.若不同捐款金额的捐款人数百分比统计结果如图所示,则该班同学平均每人捐款
(2011•资阳)在资阳市团委发起的“暖冬行动”中,某班50名同学响应号召,纷纷捐出零花钱.若不同捐款金额的捐款人数百分比统计结果如图所示,则该班同学平均每人捐款查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•资阳)如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.
(2011•资阳)如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com