
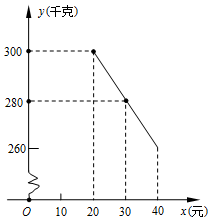
 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.分析 (1)根据函数图象经过点(20,300)和点(30,280),利用待定系数法即可求出y与x的函数关系式;
(2)根据试销期间销售单价不低于成本单价,也不高于每千克40元,结合草莓的成本价即可得出x的取值范围.
解答 解:(1)设y与x的函数关系式为y=kx+b(k≠0),
∵函数图象经过点(20,300)和点(30,280),
∴$\left\{\begin{array}{l}{20k+b=300}\\{30k+b=280}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-2}\\{b=340}\end{array}\right.$,
∴y与x的函数关系式为y=-2x+340.
(2)∵试销期间销售单价不低于成本单价,也不高于每千克40元,且草莓的成本为每千克20元,
∴自变量x的取值范围是20≤x≤40.
点评 本题考查了一次函数的应用,根据点的坐标利用待定系数法求出函数关系式是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
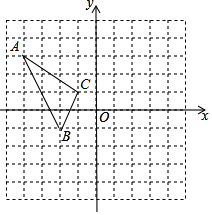 如图,在平面直角坐标系中,△ABC的顶点A(-4,3),B(-2,-1),C(-1,1)均在正方形网格的格点上,画出△ABC关于y轴对称的△A1B1C1,并写出点A的对应点A1的坐标.
如图,在平面直角坐标系中,△ABC的顶点A(-4,3),B(-2,-1),C(-1,1)均在正方形网格的格点上,画出△ABC关于y轴对称的△A1B1C1,并写出点A的对应点A1的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6cm | B. | 9cm | C. | 3cm或6cm | D. | 1cm或9cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
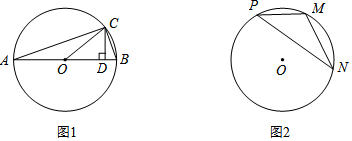
 如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )| A. | ∠M=∠N | B. | AB=CD | C. | AM=CN | D. | AM∥CN |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
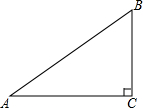 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为( )
如图,Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com