
【题目】如图,已知矩形ABCD中,AB=1,E是BC上一点,将△DCE沿DE翻折得到△DC′E.

(1) 如图1,若点B恰好在DC′的延长线上,且C′B=C′D,求CE的长;
(2) 如图2,若点A恰好在EC′的延长线上,且C′A=2C′E,求BE的长.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】
(1)由折叠得到C′D=CD=1,得到BD=2,进而得到BC=![]() ,设CE=C′E=x,则BE=
,设CE=C′E=x,则BE=![]() -x,然后在Rt△BC′E中使用勾股定理即可求解.
-x,然后在Rt△BC′E中使用勾股定理即可求解.
(2)连接DE,由折叠得∠DEC=∠DEA,又∠DEC=∠ADE,得到∠DEA=∠ADE,得到△ADE为等腰三角形,设CE= C′E=y,则AE=AD=BC=3y,得到BE=2y,在Rt△ABE中使用勾股定理即可求解.
解:(1)∵四边形ABCD是矩形,∴CD=AB=1,∠C=90°
∵△DCE沿DE翻折得到△DC′E,∴CE=C′E,C′D=CD,∠EC′D=∠C=90°
∵C′B=C′D=C′D=CD=AB=1
∴BD=2,
在Rt△BCD中,由勾股定理可知BC=![]()
设CE=C′E=x,则BE=![]() -x
-x
在Rt△BC′E中,由勾股定理有:![]()
代入数据:![]()
解得:![]() ,即CE=
,即CE=![]()
故答案为:![]() .
.
(2)连接DE,如下图所示:

由折叠得∠DEC=∠DEA,
又∵AD∥BC,∴∠ADE=∠DEC
∴∠DEA=∠ADE
∴△ADE为等腰三角形
∴AE=AD
设CE= C′E=y,则AC′=2C′E =2y
∴BC=AD=AE= AC′+ C′E =2y+y=3y,
∴BE=BC-CE=3y-y=2y
在Rt△ABE中,由勾股定理得:![]()
代入数据得:![]()
解得:![]() ,即BE =2y=
,即BE =2y=![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法中:①0是最小的整数;②有理数不是正数就是负数;③正整数、负整数、正分数、负分数统称为有理数;④非负数就是正数;④![]() 不仅是有理数,而且是分数;⑤
不仅是有理数,而且是分数;⑤![]() 是无限不循环小数,所以不是有理数;⑥无限小数不都是有理数;⑦正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )
是无限不循环小数,所以不是有理数;⑥无限小数不都是有理数;⑦正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )
A. 7个B. 6个C. 5个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张丘建,我国南北朝时期(约公元5世纪)著名的数学家,著有《张丘建算经》.一次宴会上,张丘建出了一道题:“现有一只鹿向西跑,当猎人追至![]() 处时,与鹿所在的
处时,与鹿所在的![]() 处还差36步(古代:1里=300步);鹿突然向北跑,此时骑马的猎人就沿着
处还差36步(古代:1里=300步);鹿突然向北跑,此时骑马的猎人就沿着![]() 追去,追了50步至
追去,追了50步至![]() 处与鹿所在的位置
处与鹿所在的位置![]() 处还差10步(点
处还差10步(点![]() 、
、![]() 、
、![]() 在同一直线上).如果此鹿不向北转,而继续向西跑,猎人需要追多远才能追上此鹿?”,已知单位时间内鹿跑的路程和猎人骑马追赶的路程的比值是定值,请解答这个问题.
在同一直线上).如果此鹿不向北转,而继续向西跑,猎人需要追多远才能追上此鹿?”,已知单位时间内鹿跑的路程和猎人骑马追赶的路程的比值是定值,请解答这个问题.


查看答案和解析>>
科目:初中数学 来源: 题型:
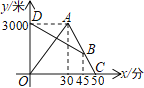
【题目】某天早晨,小童从家跑步去体育场锻炼,同时小郑从体育场晨练结束回家,途中两人相遇.小童跑到体育场后发现要下雨,立即按原路返回,遇到小郑后两人一起回到家(小童和小郑始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与小童出发的时间x(分)之间的函数图象.当x=_______时,小童与小郑相距600米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=2x+4交x轴于A,交y轴于B.

(1) 直接写出直线l向右平移2个单位得到的直线l1的解析式_______;
(2) 直接写出直线l关于y=-x对称的直线l2的解析式_______;
(3) 点P在直线l上,若S△OAP=2S△OBP,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x 轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为2的等边三角形ABC的顶点C作直线l⊥ BC,然后作△ABC关于直线l对称的△A′B′C,P为线段A′C上一动点,连接AP,PB,则AP+PB的最小值是 ( )
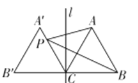
A.4B.3C.2D.2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线![]() 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为_______。
的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为_______。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com