
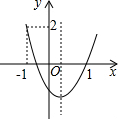
 如图,二次函数y=ax2+bx+c的图象,图象经过点(-1,2)和(1,0),给出四个结论:
如图,二次函数y=ax2+bx+c的图象,图象经过点(-1,2)和(1,0),给出四个结论:分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:由抛物线的开口方向向上可推出a>0;
因为对称轴在y轴右侧,对称轴为x=-$\frac{b}{2a}$>0,
又∵a>0,
∴b<0;
∵抛物线与y轴的交点在y轴的负半轴上,
∴c<0,故abc>0,
故①错误;
∵由图象可知:对称轴x=-$\frac{b}{2a}$>0且对称轴x=-$\frac{b}{2a}$<1,
∴-b<2a,∴2a+b>0,
故②正确;
∵由题意可知:当x=-1时,y=2,∴a-b+c=2,
当x=1时,y=0,∴a+b+c=0.
a-b+c=2与a+b+c=0相加得2a+2c=2,即a+c=1,移项得a=1-c,
又∵a>0,c<0,
∴a>1,
故③④正确.
∵a>0,c<0,
∴-3a<0,4c<0,
∴-3a+4c<0,
∵0<-$\frac{b}{2a}$<1,
∴b>-2a,
∴9a+6b+4c<9a-12a+4c=-3a+4c<0,即9a+6b+4c<0.
故⑤错误.
故答案是:②③④.
点评 主要考查图象与二次函数系数之间的关系,难度不大,做题的关键是画出图形,题图结合认真分析出a,b,c的符号.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com