
某工厂现有甲种原料360kg,乙种原料290kg,计划用它们生产A、B两种产品共50件,已知每生产一件A种产品,需要甲种原料9kg、乙种原料3kg,获利700元,生产一件B种产品,需要甲种原料4kg、乙种原料10kg,可获利1200元.
(1)利用这些原料,生产A、B两种产品,有哪几种不同的方案?
(2)设生产两种产品总利润为y(元),其中生产A中产品x(件),试写出y与x之间的函数解析式.
(3)利用函数性质说明,采用(1)中哪种生产方案所获总利润最大?最大利润是多少?
(1)符合的生产方案有三种,分别为①生产A产品30件,B产品20件;②生产A产品31件,B产品19件;③生产A产品32件,B产品18件;(2)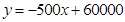 ;(3)第一种方案,45000.
;(3)第一种方案,45000.
解析试题分析:(1)关系式为:A种产品需要甲种原料数量+B种产品需要甲种原料数量≤360;A种产品需要乙种原料数量+B种产品需要乙种原料数量≤290,把相关数值代入即可;解不等式,得到关于x的范围,根据整数解可得相应方案
(2)总获利=700×A种产品数量+1200×B种产品数量;
(3)根据函数的增减性和(1)得到的取值可得最大利润.
试题解析:(1)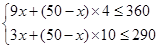 ;解第一个不等式得:
;解第一个不等式得: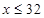 ,解第二个不等式得:
,解第二个不等式得: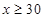 ,∴
,∴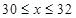 ,∵
,∵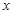 为正整数,∴
为正整数,∴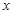 =30、31、32,∴50﹣30=20,50﹣31=19,50﹣32=18,∴符合的生产方案有三种,分别为①生产A产品30件,B产品20件;②生产A产品31件,B产品19件;③生产A产品32件,B产品18件;
=30、31、32,∴50﹣30=20,50﹣31=19,50﹣32=18,∴符合的生产方案有三种,分别为①生产A产品30件,B产品20件;②生产A产品31件,B产品19件;③生产A产品32件,B产品18件;
(2)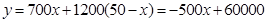 ,
,
(3)∵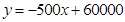 ,﹣500<0,而
,﹣500<0,而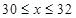 ,∴当
,∴当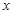 越小时,总利润
越小时,总利润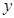 越大,即当
越大,即当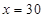 时,最大利润为:
时,最大利润为: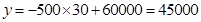 元.∴生产A产品30件,B产品20件使生产A、B两种产品的总获利最大,最大利润是45000元.
元.∴生产A产品30件,B产品20件使生产A、B两种产品的总获利最大,最大利润是45000元.
考点:1.一元一次不等式组的应用;2.方案型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行,并以各自的速度匀速行驶,途径配货站C,甲车先到达C地,并在C地用1小时配货,然后按原速度开往B地,乙车从B地直达A地,下图是甲、乙两车间的距离 (千米)与乙车出发
(千米)与乙车出发 (时)的函数的部分图像.
(时)的函数的部分图像.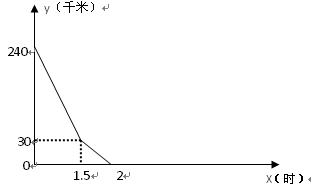
(1)A、B两地的距离是 千米,乙车出发 小时与甲相遇;
(2)求乙车出发1.5小时后直至到达A地的过程中,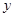 与
与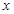 的函数关系式及
的函数关系式及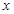 的取值范围;
的取值范围;
(3)乙车出发多长时间,两车相距100千米?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式图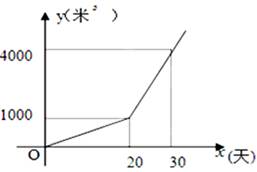
(1)第20天的总用水量为多少米3?
(2)当x≥20时,求y与x之间的函数关系式;
(3)种植时间为多少天时,总用水量达到7000米3?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知一次函数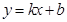 的图象经过点
的图象经过点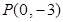 ,且与函数
,且与函数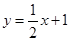 的图象相交于点
的图象相交于点 .
.
(1)求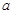 的值;
的值;
(2)若函数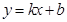 的图象与
的图象与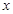 轴的交点是B,函数
轴的交点是B,函数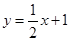 的图象与
的图象与 轴的交点是C,求四边形
轴的交点是C,求四边形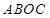 的面积(其中O为坐标原点).
的面积(其中O为坐标原点).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.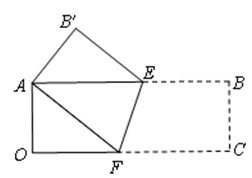
(2)实践与应用:以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),请求出折痕EF的长及EF所在直线的函数关系式.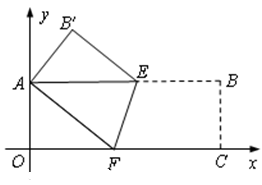
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川南充8分)某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: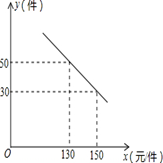
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与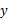 轴交于点B,且OA=OB,求这两个函数的关系式及两直线与
轴交于点B,且OA=OB,求这两个函数的关系式及两直线与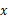 轴围成的三角形的面积.
轴围成的三角形的面积. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com