
【题目】如图,已知正方形ABCD的边长为10cm,点E在边AB上,且AE=4cm,

(1)如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为________cm/s时,在某一时刻也能够使△BPE与△CQP全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD的四条边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在何处?
【答案】(1)是,4.8;(2)经过![]() 秒点P与点Q第一次在A点相遇.
秒点P与点Q第一次在A点相遇.
【解析】
试题正方形的四边相等,四个角都是直角.(1)①速度相等,运动的时间相等,所以距离相等,根据全等三角形的判定定理可证明.②因为运动时间一样,运动速度不相等,所以BP≠CQ,只有BP=CP时才相等,根据此可求解.
(2)知道速度,知道距离,这实际上是个追及问题,可根据追及问题的等量关系求解.
试题解析:(1)①∵t=1秒,
∴BP=CQ=4×1=4厘米,
∵正方形ABCD中,边长为10厘米
∴PC=BE=6厘米,
又∵正方形ABCD,
∴∠B=∠C,
∴△BPE≌△CQP
②∵VP≠VQ,∴BP≠CQ,
又∵△BPE≌△CQP,∠B=∠C,则BP=PC,
而BP=4t,CP=10-4t,
∴4t=10-4t
∴点P,点Q运动的时间t=![]() 秒,
秒,
∴vq=6÷![]() =4.8厘米/秒.
=4.8厘米/秒.
(2)设经过x秒后点P与点Q第一次相遇,
由题意,得4.8x-4x=30,
解得x=![]() 秒.
秒.
∴点P共运动了![]() ×4=150厘米
×4=150厘米
∴点P、点Q在A点相遇,
∴经过![]() 秒点P与点Q第一次在A点相遇.
秒点P与点Q第一次在A点相遇.


科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现
小明在学习鲁教版八年级上册97页例4时,受到启发进行如下数学实验操作:
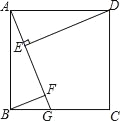
如图1,取一个锐角为45°的三角尺,把锐角顶点放在正方形ABCD的顶点D处,将三角尺绕点D旋转一个角度,使三角尺的直角边与斜边分别交边AB,BC于点E和点F,连接FE,在绕点D旋转过程中,发现线段AE,EF,CF满足EF=AE+CF的数量关系,但是不会进行证明,数学张老师给他如下的提示:把△ADE绕点D逆时针旋转90°至△DCE’的位置,小明画旋转后的图形,利用全等的知识证明了出来.你根据上面的提示画出旋转后的图形,并将上面的结论进行证明.



问题探究
小明的探究引发了老师的兴趣,老师将三角尺绕点D旋转到如图2的位置,三角尺的直角边与斜边分别交边AB,BC的延长线于点E和点F,老师问题小明此时AE,EF,CF满足什么数量关系,小明思考后说出了正确的结论.请同学们直接写出正确结论(不用写出证明过程).
拓展延伸
张老师让小明利用上面探究积累的学习经验,解答下面的问题:
如图3已知正方形ABCD,点E在边AB上,点F在边BC上,且∠EDF=45°,若CD=6,AE=2,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)如图1,求证:AE=BF;
(2)连接DF,若tan∠BAG=![]() ,AB=2
,AB=2![]() ,求△ADF的面积.
,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
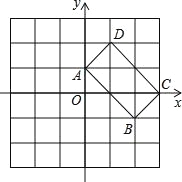
【题目】如图,在 6×6 的网格中,四边形 ABCD 的顶点都在格点上,每个格子都是边长为 1 的正方形,建立如图所示的平面直角坐标系.
(1)画出四边形 ABCD 关于 y 轴对称和四边形 A′B′C′D′(点 A、B、C、D的对称点分别是点 A′B′C′D′.
(2)求 A、B′、B、C 四点组成和四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书.第一次用![]() 元购书若干本,并按该书定价
元购书若干本,并按该书定价![]() 元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了
元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了![]() ,他用
,他用![]() 元所购该书数量比第一次多
元所购该书数量比第一次多![]() 本.
本.
(1)求两次购书的价格分别是多少?
(2)若第二次购书按定价售出![]() 本时,出现滞销,于是决定打折出售剩下这批书,那么该商家最低打几折才能保证剩下书的利润率不低于
本时,出现滞销,于是决定打折出售剩下这批书,那么该商家最低打几折才能保证剩下书的利润率不低于![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知双曲线y=![]() (x<0)和y=
(x<0)和y=![]() (x>0),直线OA与双曲线y=
(x>0),直线OA与双曲线y=![]() 交于点A,将直线OA向下平移与双曲线y=
交于点A,将直线OA向下平移与双曲线y=![]() 交于点B,与y轴交于点P,与双曲线y=
交于点B,与y轴交于点P,与双曲线y=![]() 交于点C,S△ABC=6,
交于点C,S△ABC=6,![]() =
=![]() ,则k=( )
,则k=( )

A. ﹣6 B. ﹣4 C. 6 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AB边上一点,E为CD中点,AC=![]() ,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )

A. ![]() B.
B. ![]() +1﹣
+1﹣![]() C.
C. ![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com