
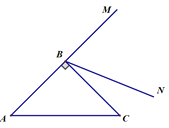
【题目】如图,BN是等腰Rt△ABC的外角∠CBM内部的一条射线,∠ABC=90°,AB=CB,点C关于BN的对称点为D,连接AD,BD,CD,其中CD,AD分别交射线BN于点E,P.
(1)依题意补全图形;
(2)若∠CBN=![]() ,求∠BDA的大小(用含
,求∠BDA的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示线段PB,PA与PE之间的数量关系,并证明.
【答案】(1)补图见解析;(2)45°-![]() ;(3)PA=
;(3)PA=![]() (PB+PE)..
(PB+PE)..
【解析】
此题涉及的知识点是对称点的画法,角大小的求解,数量关系的证明,解答时第一问根据已知条件直接画图,连线;第二问根据对称图形性质可以算出角的大小;第三问证明两三角形全等就可以得到线段之间的关系。
解:(1) 如图所示:
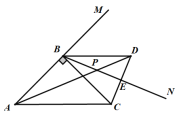
(2)∵∠ABC=90°
∴∠MBC=∠ABC=90°
∵点C关于BN的对称点为D
∴BC=BD,∠CBN=∠DBN=![]()
∵AB=BC
∴AB=BD
∴∠BAD=∠ADB=![]() =45°-
=45°-![]()
(3)猜想:![]()
证明:
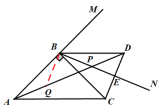
过点B作BQ⊥BE交AD于Q
∵∠BPA=∠DBN+∠ADB,∠ADB=45°-![]() ,∠DBN=
,∠DBN=![]()
∴∠BPA=∠DPE=45°
∵点C关于BN的对称点为D
∴BE⊥CD
∴PD=![]() PE,PQ=
PE,PQ=![]() PB,
PB,
∵BQ⊥BE,∠BPA=45°
∴∠BPA=∠BQP=45°
∴∠AQB=∠DPB=135°
又∵AB=BD,∠BAD=∠ADB
∴△AQB≌△BPD(AAS)
∴AQ=PD
∵PA=AQ+PQ
∴![]()


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】为了更好地治理水质,保护环境,某污水处理公司决定购买10台污水处理设备,现有A、B两种设备可供选择,月处理污水分别为240m3/月、200m3/月.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少8万元.
(1)A、B两种型号的设备每台的价格是多少?
(2)若污水处理公司购买设备的预算资金不超过125万元,你认为该公司有哪几种购买方案?
(3)若每月需处理的污水约2040m3,在不突破(2)中资金预算的前提下,为了节约资金,又要保证治污效果,请你为污水处理公司设计一种最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周六上午,小亮去图书馆查资料,图书馆离家不远,他步行去图书馆,查完资料后他又边走边转去书店买书,在书店停留了几分钟后骑共享单车回家."已知小亮离家的距离![]() (米)与离开家的时间
(米)与离开家的时间![]() (分)之间的关系如图所示.请根据图象回答下列问题:
(分)之间的关系如图所示.请根据图象回答下列问题:
(1)小亮出发几分钟后到达图书馆?
(2)小亮查完资料后步行的速度是多少?
(3)小亮![]() 离开图书馆,几点回到家?
离开图书馆,几点回到家?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A,B,C,D是四个小城镇,除BC外,它们之间都有笔直的公路连接,公共汽车行驶于城镇之间,其票价与路程成正比.已知各城镇间的公共汽车票价如下: A——B:10元;A——C:12.5元;A——D:8元; B——D:6元;C——D:4.5元.为了方便B,C之间的交通,在B,C之间建成一条笔直的公路,请按上述标准计算出B,C之间公共汽车的票价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(3,0),与y轴交于点C(0,3).
(1)求该抛物线所对应的函数关系式;
(2)设抛物线上的一个动点P的横坐标为t(0<t<0),过点P作PD⊥BC于点D.
①求线段PD的长的最大值;②当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.

(1)这些车的平均速度为__________千米/时;
(2)车速的众数是__________;
(3)车速的中位数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣1,下列结论中: ①ab>0,②a+b+c>0,③当﹣2<x<0时,y<0.
正确的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com