
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
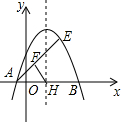 如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).
如图,抛物线y=-(x-1)2+m经过E(2,3),与x轴交于A、B两点(A在B的左侧).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
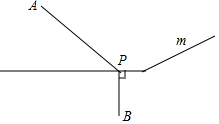 如图所示,在两个村庄A,B附近的河流可以近似地看成一条折线段(图中m)A,B分别在河的两旁,现要在河边修一个水泵站,同时向A,B两村供水,为了节约建设的费用,就要使所铺设的管道最短,某人甲提出了这样的建议:从点B向河道作垂线交m于点P,则点P为水泵站的位置.
如图所示,在两个村庄A,B附近的河流可以近似地看成一条折线段(图中m)A,B分别在河的两旁,现要在河边修一个水泵站,同时向A,B两村供水,为了节约建设的费用,就要使所铺设的管道最短,某人甲提出了这样的建议:从点B向河道作垂线交m于点P,则点P为水泵站的位置.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
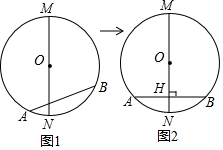
 如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )| A. | 12π-16$\sqrt{7}$ | B. | 16π-18$\sqrt{7}$ | C. | 16π-24$\sqrt{7}$ | D. | 16π-12$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
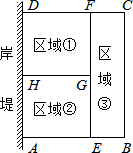 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com