
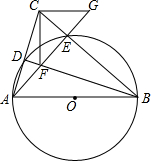
 如图所示,△ABC中,AB是⊙O的直径,AC和BC分别和⊙O相交于点D和E,在BD上截取BF=AC,延长AE使AG=BC.求证:
如图所示,△ABC中,AB是⊙O的直径,AC和BC分别和⊙O相交于点D和E,在BD上截取BF=AC,延长AE使AG=BC.求证:分析 (1)根据圆周角定理可得∠CAG=∠FBC,根据SAS证明△CAG≌△FBC,再根据全等三角形的性质可证CG=CF;
(2)根据直径所对的圆心角为90°,根据全等三角形的性质和等量关系可知CG⊥CF.
解答 证明:(1)由圆周角定理可得∠CAG=∠FBC,
在△CAG与△FBC中,
$\left\{\begin{array}{l}{BF=AC}\\{∠CAG=∠FBC}\\{AG=BC}\end{array}\right.$,
∴△CAG≌△FBC(SAS),
∴CG=CF;
(2)∵AB是⊙O的直径,
∴∠CEG=∠AEB=90°,
∴∠G+∠GCE=90°,
∵△CAG≌△FBC,
∴∠G=∠BCF,
∴∠BCF+∠GCE=90°,
∴CG⊥CF.
点评 此题考查了全等三角形的判定与性质,圆周角定理,直径所对的圆心角为90°,关键是证明△CAG≌△FBC.


科目:初中数学 来源: 题型:解答题
| 到A工厂 | 到B工厂 | |
| C煤场 | 每吨35元 | 每吨30元 |
| D煤场 | 每吨40元 | 每吨45元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:判断题
已知抛物线y=ax2+bx+c经过A(1,0)、B(5,0)两点,最高点纵坐标为4,与y轴交于点C.

(1)求抛物线的解析式;
(2)若△ABC的外接圆⊙O’交y轴于不同点C和D,⊙O’的弦DE平行于x轴,求直线CE的解析式;
(3)在x轴的负半轴上是否存在点F,使△OCF与△CDE相似?若存在求出符合条件的所有点F的坐标,并判定直线CF与⊙O’的位置关系;若不存在,请说明理由?
查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
在一个不透明的盒子中,放入2个白球和1个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出2个球,请通过列表或树状图求摸出2个球都是白球的概率;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋中,再次搅匀后从中任意摸出1个球,请通过列表或树状图求2次摸出的球都是白球的概率;
(3)现有一个可以自由转动的转盘,转盘被等分成60个相等的扇形,这些扇形除颜色外完全相同,其中40个扇形涂上白色,20个扇形涂上红色,转动转盘2次,指针2次都指向白色区域的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-4\frac{2}{3}>-4.7$ | B. | $-\frac{12}{23}<-\frac{6}{11}$ | C. | -0.2<-0.22 | D. | $-0.01<-\frac{1}{100}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com