
已知:如图,折叠长方形的一边AD,使点D落在BC边上的点F处,如AB=8cm,BC=10cm,求EC的长。
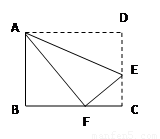
依题意可得:BC=AD=AF=10,DE=EF.
在△ABF中,∠ABF=90°.
∴BF=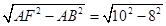 =6,
=6,
∴FC=10-6=4,
设EC=x,则EF=DE=8-x.
∵∠C=90°,
∴EC2+FC2=EF2,
∴x2+42=(8-x)2,
解之得:x=3,
∴EC=3(cm).
【解析】要求CE的长,就必须求出DE的长,如果设EC=x,那么我们可将DE,EC转化到一个三角形中进行计算,根据折叠的性质我们可得出AD=AF,DE=EF,那么DE,CE就都转化到直角三角形EFC中了,下面的关键就是求出FC的长,也就必须求出BF的长,我们发现直角三角形ABF中,已知了AB的长,AF=AD=10,因此可求出BF的长,也就有了CF的长,在直角三角形EFC中,可用勾股定理,得出关于x的一元二次方程,进而求出未知数的值.


科目:初中数学 来源: 题型:
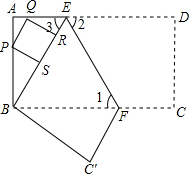 已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.查看答案和解析>>
科目:初中数学 来源:双色笔记八年级数学上(北京师大版) 题型:044
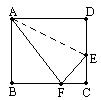
已知:如图,折叠长方形(四个角都是直角,对边相等的四边形)的一边AD,使点D落在BC边的点F处,若AB=8cm,BC=10cm,求EC的长.
查看答案和解析>>
科目:初中数学 来源:同步单元练习 数学八年级 上册 题型:044
已知:如图,折叠长方形(四个角都是直角,对边相等)的一边AD,折痕为AE,点D落在BC边的点F处.已知AB=8cm,BC=10cm.求CE的长.

查看答案和解析>>
科目:初中数学 来源:2011--2012学年安徽省定远中学八年级下学期期中数学试卷(带解析) 题型:解答题
已知:如图,折叠长方形的一边AD,使点D落在BC边上的点F处,如AB=8cm,BC=10cm,求EC的长。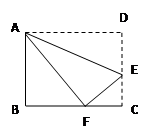
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com