
【题目】一个四边形被一条对角线分割成两个三角形,如果被分割的两个三角形相似,我们把这条对角线称为该四边形的为相似对角线。
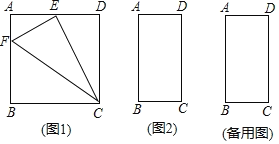
(1)如图1,正方形ABCD的边长为4,E为AD的中点,AF=1,连结CE,CF,求证:EF为四边形AECF的相似对角线。
(2)在四边形ABCD中,∠BAD=120°,AB=3,AC=![]() ,AC平分∠BAD,且AC是四边形ABCD的相似对角线,求BD的长。
,AC平分∠BAD,且AC是四边形ABCD的相似对角线,求BD的长。
(3)如图2,在矩形ABCD中,AB=6,BC=4,点E是线段AB(不取端点A,B)上的一个动点,点F是射线AD上的一个动点,若EF是四边形AECF的相似对角线,求BE的长.(直接写出答案)
【答案】(1)见解析 (2)3![]() 或
或![]() . (3)
. (3)![]() 或3
或3
【解析】
(1)如图1中,只要证明△AEF∽△ECF即可解决问题;
(2)如图2、图3中,AC是四边形ABCD的相似对角线,有两种情形:①如图2中,△ACB≌△ACD时.②如图3中,当△ACD∽△ABC时,分别求解即可;
(3)分三种情形①如图4中,当△AEF和△CEF关于EF对称时,EF是四边形AECF的相似对角线.②如图5中,如图取AD中点F,连接CF,将△CFD沿CF翻折得到△CFD′,延长CD′交AB于E,易证EF是四边形AECF的相似对角线.③如图6中,取AB的中点E,连接CE,作EF⊥AD于F,延长CB交FE的延长线于M,则易证EF是四边形AECF的相似对角线.此时BE=3;
(1)如图1中,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,
∵AE=DE=2,AF=1,
∴![]() ,
,
∵∠A=∠D=90°,
∴△AEF∽△DCE,
∴∠AEF=∠DCE,![]() ,
,
∵∠DCE+∠CED=90°,
∴∠AEF+∠CED=90°,
∴∠FEC=∠A=90°,
∵![]() ,
,
∴![]() ,
,
∴△AEF∽△ECF,
∴EF为四边形AECF的相似对角线.
(2)如图2中,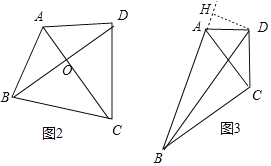
∵AC是四边形ABCD的相似对角线,
∴有两种情形:
①如图2中,△ACB≌△ACD时,∵AB=AD=3,BC=CD,
∴AC垂直平分DB,
在Rt△AOB中,∵AB=3,∠ABO=30°,
∴BO=ABcos30°=![]() ,
,
∴BD=2OB=3![]() .
.
②如图3中,当△ACD∽△ABC时,可得AC2=ABAD,
∴6=3AD,
∴AD=2,
在Rt△ADH中,∵∠HAD=60°,AD=2,
∴AH=![]() AD=1,DH=
AD=1,DH=![]() AH=
AH=![]() ,
,
在Rt△BDH中,BD=![]() .
.
综上所述,BD=3![]() 或
或![]() .
.
(3)①如图4中,当△AEF和△CEF关于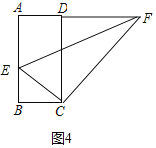
设AE=EC=x,
在Rt△BCE中,∵EC2=BE2+BC2,
∴x2=(6-x)2+42,解得x=![]() ,
,
∴此时BE=AB-AE=6-![]() .
.
②如图5中,如图取AD中点F,连接CF,将△CFD沿CF翻折得到△CFD′,延长CD′交AB于E,易证EF是四边形AECF的相似对角线.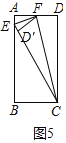
由△AEF∽△DFC得到,![]() ,
,
∴![]() ,
,
∴AE=![]() ,
,
∴BE=AB-AE=![]() .
.
③如图6中,取AB的中点E,连接CE,作EF⊥EC交AD于F,延长CB交FE的延长线于M,则易证EF是四边形AECF的相似对角线.此时BE=3.
综上所述,满足条件的BE的值为![]() 或3.
或3.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】某商店从厂家以21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为![]() 元,则可卖出(350-10
元,则可卖出(350-10![]() )件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
)件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A,C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E,F,则四边形EMFD面积的最大值为( )
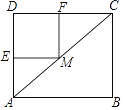
A. 6 B. 12 C. 18 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡,为了集中光线,加上了灯罩(如图所示).已知灯罩深AN=8cm,灯泡离地面2m,为了使光线恰好照在墙角D、E处,灯罩的直径BC应为多少?(结果保留两位小数,![]() ≈1.414)
≈1.414)
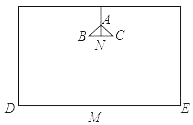
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司2017年初刚成立时投资1000万元购买新生产线生产新产品,此外,生产每件该产品还需要成本40元.按规定,该产品售价不得低于60元/件且不超过160元/件,且每年售价确定以后不再变化,该产品的年销售量![]() (万件)与产品售价
(万件)与产品售价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)求2017年该公司的最大利润?
(3)在2017年取得最大利润的前提下,2018年公司将重新确定产品售价,能否使两年共盈利达980万元.若能,求出2018年产品的售价;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABD中,AB=AD,点M 为边AD上一动点,点E在DA的延长线上,且AM=AE,以BE为直角边,向外作等腰Rt△BEG,MG交AB于N,连NE、DN.
(1)求证:∠BEN=∠BGN.
(2)求![]() 的值.
的值.
(3)当M在AD上运动时,探究四边形BDNG的形状,并证明之.
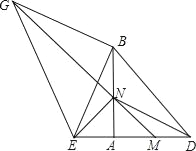
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.
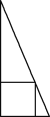
查看答案和解析>>
科目:初中数学 来源: 题型:
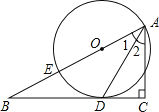
【题目】如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com