
【题目】在△ABC中,已知∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O,∠BOC的平分线交BC于F,有下列结论:①∠BOE=60°,②∠ABD=∠ACE,③OE=OD,④BC=BE+CD。其中正确的是_________。(把所有正确结论的序号都选上)
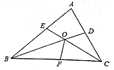
【答案】①③④
【解析】
①正确.根据外角的性质得:∠BOE=∠OBC+∠OCB=60°;
②不正确.∠ABD=![]() ∠ABC,∠ACE=
∠ABC,∠ACE=![]() ∠ACB,当AB=AC时,∠ABC=∠ACB,才有∠ABD=∠ACE;
∠ACB,当AB=AC时,∠ABC=∠ACB,才有∠ABD=∠ACE;
③只要证明△BOE≌△BOF,△CDO≌△CFO,即可解决问题;
④根据③中的三角形全等,可得对应边相等,相加可得结论.
解:①如图,∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵BD、CE分别是∠ABC和∠BCA的平分线,
∴∠OBC+∠OCB=![]() ×120°=60°,
×120°=60°,
∴∠BOE=∠OBC+∠OCB=60°
故①正确;
②∵BD、CE分别是∠ABC和∠BCA的平分线,
∴∠ABD=![]() ∠ABC,∠ACE=
∠ABC,∠ACE=![]() ∠ACB,
∠ACB,
当AB=AC时,∠ABC=∠ACB,
而已知AB和AC没有相等关系,
故②不正确;
③∵∠OBC+∠OCB=60°,
∴∠BOC=120°,
∵OF平分∠BOC,
∴∠BOF=∠COF=60°,
∴∠BOE=60°,
∴∠BOE=∠BOF,
在△BOE和△BOF中,
∵
∴△BOE≌△BOF(ASA),
∴OE=OF,
同理得:△CDO≌△CFO,
∴OD=OF,
∴OD=OE,
故③正确;
④∵△BOE≌△BOF,△CDO≌△CFO,
∴BF=BE,CF=CD,
∴BC=CF+BF=BE+CD,
故④正确;
则下列说法中正确的是:①③④
故答案为①③④.


科目:初中数学 来源: 题型:
【题目】一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.如图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的 ![]() 的概率是 .
的概率是 . 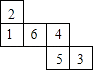
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直线
为直线![]() 上一点,
上一点,![]() 为直线
为直线![]() 上一点,
上一点,![]()

(1)如图1,当![]() 在
在![]() 上,
上,![]() 在
在![]() 上时,求证
上时,求证![]() ;
;
(2)如图2,当![]() 在
在![]() 的延长线上,
的延长线上,![]() 在
在![]() 的延长线上时,点
的延长线上时,点![]() 在
在![]() 上,连接
上,连接![]() ,且
,且![]() ,求证:
,求证:![]()
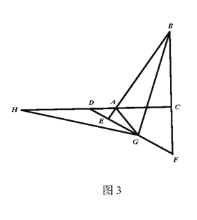
(3)如图3,在(2)的条件下,连接![]() 当
当![]() 平分
平分![]() 时,将
时,将![]() 沿着
沿着![]() 折至
折至![]() 探究
探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
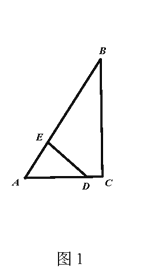
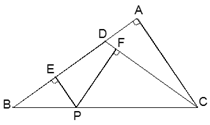
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC。若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,D是BC上的一点,且满足∠BAD= ![]() ∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
(1)求证:直线BC是⊙O的切线;
(2)连接EF,若tan∠AEF= ![]() ,AD=4,求BD的长.
,AD=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
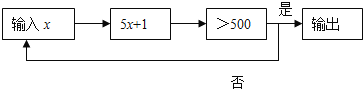
【题目】按下面程序计算,即根据输入的![]() 判断
判断![]() 是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的
是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的![]() 的值作为新的
的值作为新的![]() 的值,继续运算,循环往复,直至输出结果为止.若开始输入
的值,继续运算,循环往复,直至输出结果为止.若开始输入![]() 的值为正整数,最后输出的结果为656,则满足条件的所有
的值为正整数,最后输出的结果为656,则满足条件的所有![]() 的值是__.
的值是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A、B、C在同一条直线上,点M为线段AC的中点、点N为线段BC的中点.
(1)如图,当点C在线段AB上时:
①若线段![]() ,求
,求![]() 的长度.
的长度.
②若AB=a,求MN的长度.
(2)若![]() ,求MN的长度(用含
,求MN的长度(用含![]() 的代数式表示).
的代数式表示).
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com