练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列运算正确的是（　　）

    　

    A．

    a3+a3=a6

    B．

    a6÷a2=a4

    C．

    a3•a5=a15

    D．

    （a3）4=a7


    B


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图所示的正三棱柱，它的主视图是（　　）

    　   A．                                               B．                                  C．    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，四边形OABC的顶点O为坐标原点，点C在x轴的正半轴上，且BC⊥OC于点C，点A的坐标为（2，2），AB=4，∠B=60°，点D是线段OC上一点，且OD=4，连接AD．

    （1）求证：△AOD是等边三角形；

    （2）求点B的坐标；

    （3）平行于AD的直线l从原点O出发，沿x轴正方向平移．设直线l被四边形OABC截得的线段长为m，直线l与x轴交点的横坐标为t．

    ①当直线l与x轴的交点在线段CD上（交点不与点C，D重合）时，请直接写出m与t的函数关系式（不必写出自变量t的取值范围）

    ②若m=2，请直接写出此时直线l与x轴的交点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解不等式x﹣1≤x﹣，并把它的解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


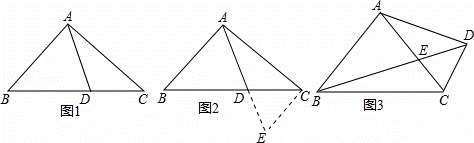
    阅读下面材料：小腾遇到这样一个问题：如图1，在△ABC中，点D在线段BC上，∠BAD=75°，∠CAD=30°，AD=2，BD=2DC，求AC的长．

    小腾发现，过点C作CE∥AB，交AD的延长线于点E，通过构造△ACE，经过推理和计算能够使问题得到解决（如图 2）．

    请回答：∠ACE的度数为　　，AC的长为　 　．

    参考小腾思考问题的方法，解决问题：

    如图 3，在四边形 ABCD中，∠BAC=90°，∠CAD=30°，∠ADC=75°，AC与BD交于点E，AE=2，BE=2ED，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于（　　）

    　

    A．

    40°

    B．

    50°

    C．

    70°

    D．

    80°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若一组数据3，4，x，5，8的平均数是4，则该组数据的中位数是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知⊙O1与⊙O2的半径分别是2和4，O1O2=5，则⊙O1与⊙O2的位置关系是（　　）

    　

    A．

    内含

    B．

    内切

    C．

    相交

    D．

    外切

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

    （1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是　 　；

    （2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是　 　；

    （3）△A2B2C2的面积是　 　平方单位．

    查看答案和解析>>

    同步练习册答案