
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC﹣b,AB=c.
【特例探索】
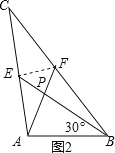
(1)如图1,当∠ABE=45°,c=2![]() 时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
【拓展应用】
(3)如图4,在ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2![]() ,AB=3.求AF的长.
,AB=3.求AF的长.

【答案】(1)a=2![]() ,b=2
,b=2![]() ; a=2
; a=2![]() ,b=2
,b=2![]() ;(2)见解析;(3)4.
;(2)见解析;(3)4.
【解析】试题分析:(1)由等腰直角三角形的性质得到![]() 根据三角形中位线的性质,得到
根据三角形中位线的性质,得到![]() ,
, ![]() 再由勾股定理得到结果;
再由勾股定理得到结果;
(2)连接EF,设PF=m,PE=n则AP=2m,PB=2n,类比着(1)即可证得结论.
(3)连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,由点E.G分别是AD,CD的中点,得到EG是△ACD的中位线,于是证出![]() 由四边形ABCD是平行四边形,得到
由四边形ABCD是平行四边形,得到![]() ,
, ![]() ∠EAH=∠FCH根据E,F分别是AD,BC的中点,得到
∠EAH=∠FCH根据E,F分别是AD,BC的中点,得到![]() 证出四边形ABFE是平行四边形,证得EH=FH,推出EP,AH分别是△AFE的中线,由(2)的结论得即可得到结果.
证出四边形ABFE是平行四边形,证得EH=FH,推出EP,AH分别是△AFE的中线,由(2)的结论得即可得到结果.
试题解析![]()
![]()
∵AF,BE是△ABC的中线,
∴![]() ,
, ![]()
![]()
∴PE=PF=1,
在Rt△FPB和Rt△PEA中,
![]()
![]()
![]()
如图2,连接EF,
同理可得: ![]()
∵![]()
∴△PEF△ABP,
![]()
在Rt△ABP中,
![]()
![]()
![]()
在Rt△APE和Rt△BPF中,
![]()
![]()
故答案为: ![]()
(2)猜想: ![]() 三者之间的关系是:
三者之间的关系是: ![]()
证明:如图3,连接EF,∵AF,BE是△ABC的中线,
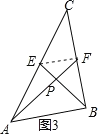
∴EF是△ABC的中位线,
∴![]() .且
.且![]()
![]()
设PF=m,PE=n则AP=2m,PB=2n,
在Rt△APB中, ![]() ①
①
在Rt△APE中, ![]() ②
②
在Rt△BPF中, ![]() ③
③
由①得: ![]() 由②+③得:
由②+③得: ![]()
![]()
(3)如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,
∵点E.G分别是AD,CD的中点,
∴![]() ,
,
∵BE⊥EG,
∴BE⊥AC,
∵四边形ABCD是平行四边形,
∴![]() ,
, ![]()
∴∠EAH=∠FCH,
∵E,F分别是AD,BC的中点,
![]()
![]()
∵![]() ,
,
∴四边形ABFE是平行四边形,
∴EF=AB=3,AP=PF,
在△AEH和△CFH中, 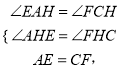
∴△AEH≌△CFH,
∴EH=FH,
∴EP,AH分别是△AFE的中线,
由(2)的结论得: ![]()
![]()
∴AF=4.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
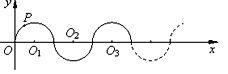
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点P的坐标是________________
个单位长度,则第2019秒时,点P的坐标是________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 是
是![]() 轴上一动点,要使点
轴上一动点,要使点![]() 关于直线
关于直线![]() 的对称点刚好落在
的对称点刚好落在![]() 轴上,则此时点
轴上,则此时点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:
①若a>0,b>0,则a+b>0;
②若a2=b2,则a=b;
③线段垂直平分线上的点到线段两端点距离相等;
④平行四边形的对角线互相平分
其中原命题与逆命题均为真命题的是( )
A. ①③ B. ②④ C. ③④ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥BC,EG⊥BC,垂足分别为D、G、AD平分∠BAC,求证:∠E=∠4.
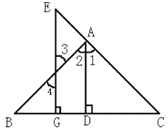
证明:∵AD⊥BC,EG⊥BC(已知)
∴AD∥EG( )
∴∠2=∠3( )
∠1= (两直线平行,同位角相等)
∵AD平分∠BAC(已知)
∴∠1=∠2( )
∴∠E=∠3( )
∵∠3=∠4( )
∴∠E=∠4(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
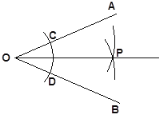
【题目】同学们已经学过用尺规作一条线段等于已知线段、作一个角等于已知角.请同学们看下面一个尺规作图的例子:
①以O为圆心,任意长为半径作弧线交∠AOB的两边OA、OB分别于C、D两点;
②以C为圆心,大于![]() CD的长为半径作弧线,再以D为圆心,同样的长为半径作弧线,两弧线交于P点;
CD的长为半径作弧线,再以D为圆心,同样的长为半径作弧线,两弧线交于P点;
③以O为端点作射线OP.
则OP就是∠AOB的平分线
你知道OP为什么是∠AOB的角平分线吗?请用你所学的知识解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日平均销售的关系如下:
销售单价(元) | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 |
日平均销售量(瓶) | 480 | 460 | 440 | 420 | 400 | 380 | 360 |
(1)若记销售单价比每瓶进价多x元,则销售量为_____(用含x的代数式表示);
求日均毛利润(日均毛利润=(每瓶售价-每瓶进价)×日均销售量-固定成本)y与x之间的函数关系式.
(2)若要使日均毛利润达到1400元,则销售单价应定为多少元?
(3)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com