
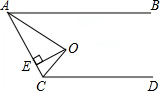
 如图,AB∥CD,O为∠BAC、∠ACD的平分线的交点,OE⊥AC于E,且OE=1,则AB与CD之间的距离等于2.
如图,AB∥CD,O为∠BAC、∠ACD的平分线的交点,OE⊥AC于E,且OE=1,则AB与CD之间的距离等于2. 科目:初中数学 来源: 题型:解答题
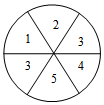 “六•一”儿童节,学校举办文艺汇演活动,小丽和小芳都相当节目主持人,但现在只有一个名额.小丽想出了一个办法,她将一个转盘(均质的)均分成6份,若图所示,游戏规定:随意转动转盘,若指针指到3,则小丽去;若指针指到2,则小芳去,这个游戏公平吗?为什么?
“六•一”儿童节,学校举办文艺汇演活动,小丽和小芳都相当节目主持人,但现在只有一个名额.小丽想出了一个办法,她将一个转盘(均质的)均分成6份,若图所示,游戏规定:随意转动转盘,若指针指到3,则小丽去;若指针指到2,则小芳去,这个游戏公平吗?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com