【题目】下列命题是真命题的是（ ）
A.三角形的三条高线相交于三角形内一点
B.等腰三角形的中线与高线重合
C.三边长为
的三角形为直角三角形
D.到线段两端距离相等的点在这条线段的垂直平分线上
科目：初中数学 来源： 题型：
【题目】如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．
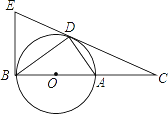
（1）求证：CD是⊙O的切线．
（2）过点B作⊙O的切线交CD的延长线于点E，若OB=5，BC=18，求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
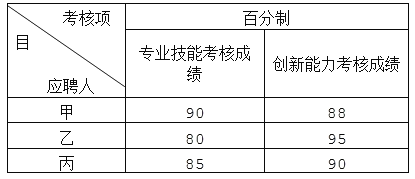
【题目】某广告公司为了招聘一名创意策划，准备从专业技能和创新能力两方面进行考核，成绩高者录取．甲、乙、丙三名应聘者的考核成绩以百分制统计如下：
（1）如果公司认为专业技能和创新能力同等重要，则应聘人 将被录取．
（2）如果公司认为职员的创新能力比专业技能重要，因此分别赋予它们6和4的权．计算他们赋权后各自的平均成绩，并说明谁将被录取．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
和
都是等腰直角三角形，
．
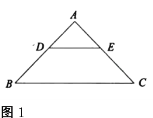
（1）如图1，点
、
分别在
、
上，则
、
满足怎样的数量关系和位置关系？（直接写出答案）
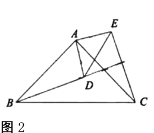
（2）如图2，点在内部，点在外部，连结、，则、满足怎样的数量关系和位置关系？请说明理由．
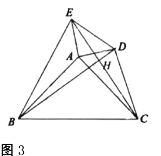
（3）如图3，点、都在外部，连结、、
、
，与相交于
点．已知
，
，设
，
，求
与
之间的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
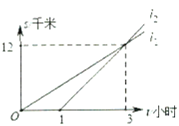
【题目】如图，
两地相距
千米，甲、乙两人都从
地去
地，图中
和
分别表示甲、乙两人所走路程
(千米)与时间
(小时)之间的关系，下列说法: ①乙晚出发
小时；②乙出发
小时后追上甲；③甲的速度是
千米/小时； ④乙先到达地.其中正确的是__________．(填序号)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题满分10分）
由于雾霾天气频发，市场上防护口罩出现热销.某药店准备购进一批口罩，已知1个A型口罩和3个B型口罩共需26元；3个A型口罩和2个B型口罩共需29元.
⑴ 求一个A型口罩和一个B型口罩的售价各是多少元？
⑵ 药店准备购进这两种型号的口罩共50个，其中A型口罩数量不少于35个，且不多于B型口罩的3倍，有哪几种购买方案，哪种方案最省钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料，解答问题．
例：用图象法解一元二次不等式：x2﹣2x﹣3＞0
解：设y=x2﹣2x﹣3，则y是x的二次函数．∵a=1＞0，∴抛物线开口向上．
又∵当y=0时，x2﹣2x﹣3=0，解得x1=﹣1，x2=3．
∴由此得抛物线y=x2﹣2x﹣3的大致图象如图所示．
观察函数图象可知：当x＜﹣1或x＞3时，y＞0．
∴x2﹣2x﹣3＞0的解集是：x＜﹣1或x＞3．
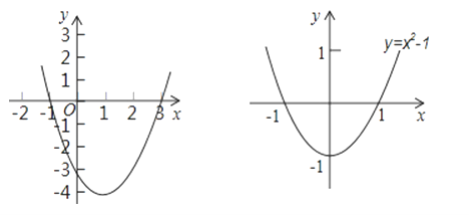
（1）观察图象，直接写出一元二次不等式：x2﹣2x﹣3＞0的解集是 ________；
（2）仿照上例，用图象法解一元二次不等式：x2﹣1＞0．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
