

分析 (1)得出考生人数,进而得出a,b,c的数值.
(2)利用平均数公式即可计算考场“声乐”科目考试的平均分.
(3)通过概率公式计算即可.
解答 解:(1)此考场的考生人数为:$\frac{10}{0.25}=40$;
a=40×0.075=3,b=$\frac{15}{40}=0.375$,c=40-3-10-15-8=4,d=$\frac{4}{40}=0.1$,
器乐考试A等3人;
(2)考生“声乐”考试平均分:(3×10+10×8+15×6+8×4+4×2)÷40=6分;
(3)因为声乐成绩为A等的有3人,器乐成绩为A等的有3人,由于本考场考试恰有2人两科均为A等,不妨记为A',A'',将声乐成绩为A等的另一人记为b,在至少一科成绩为A等考生中随机抽取两人有六种情形,两科成绩均为A等的有一种情形,所以概率为$\frac{1}{6}$.
点评 本小题主要考查统计与概率的相关知识,具体涉及到频率分布直方图、平均数及古典概型等内容.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
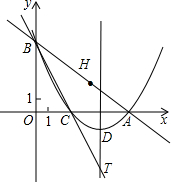 已知:如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+6与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
已知:如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+6与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AB⊥BC于B,CD⊥BC于C,AB=5,BC=8,CD=3,E为线段BC上一点.求:当AE=DE时,BE的长度,并确定此时∠AED的度数.
已知:如图,AB⊥BC于B,CD⊥BC于C,AB=5,BC=8,CD=3,E为线段BC上一点.求:当AE=DE时,BE的长度,并确定此时∠AED的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com