已知：四边形ABCD中，AC、BD交于O点，AO=OC，BA⊥AC，DC⊥AC。垂足分别为A，C。求证：AD=BC。
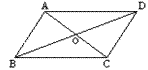
解：∵BA⊥AC，DC⊥AC
∴∠BAC=∠DCA=90°
∵AO=CO，∠1=∠2
∴△ABO≌△CDO（ASA）
∴AB=CD，∠3=∠4
∵BD=DB
∴△ABD≌△CDB（ASA）
∴AD=BC 。 |
 |
练习册系列答案
相关习题
科目：初中数学
来源：
题型：
我们给出如下定义：如果四边形中一对顶点到另一对顶点所连对角线的距离相等，则把这对顶点叫做这个四边形的一对等高点．例如：如图1，平行四边形ABCD中，可证点A、C到BD的距离相等，所以点A、C是平行四边形ABCD的一对等高点，同理可知点B、D也是平行四边形ABCD的一对等高点． （1）如图2，已知平行四边形ABCD，请你在图2中画出一个只有一对等高点的四边形ABCE（要求：画出必要的辅助线）； （2）已知P是四边形ABCD对角线BD上任意一点（不与B、D点重合），请分别探究图3、图4中S 1，S 2，S 3，S 4四者之间的等量关系（S 1，S 2，S 3，S 4分别表示△ABP，△CBP，△CDP，△ADP的面积）： ①如图3，当四边形ABCD只有一对等高点A、C时，你得到的一个结论是 ； ②如图4，当四边形ABCD没有等高点时，你得到的一个结论是 ．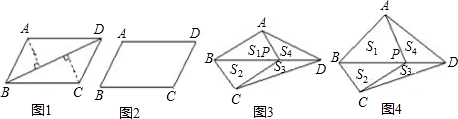 
查看答案和解析>>
科目：初中数学
来源：
题型：
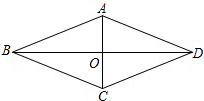 如图，已知，四边形ABCD是菱形，AC=6，BD=8，求AB的长和菱形ABCD的面积．
查看答案和解析>>
科目：初中数学
来源：
题型：
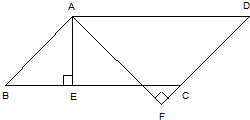 34、如图：在平行四边形ABCD中，∠B=30°，AE⊥BC于点E，AF⊥DC的延长线于点F，已知平行四边形ABCD的周长为40cm，且AE：AF=2：3．求平行四边形ABCD的面积．
查看答案和解析>>
科目：初中数学
来源：
题型：
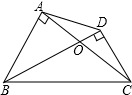 如图，已知在四边形ABCD中，AC与BD相交于点O，AB⊥AC，CD⊥BD． （1）求证：△AOD∽△BOC； （2）若 sin∠ABO=，S △AOD=4，求S △BOC的值．
查看答案和解析>>
科目：初中数学
来源：
题型：
 如图，已知平行四边形ABCD，E是边AB的中点，联结AC、DE交于点O．记向量 = ， = ，则向量 = （用向量 、 表示）．
查看答案和解析>>
|
