
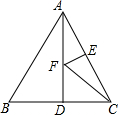
 如图,等边△ABC中,AB=4,AD⊥BC于点D,点F在线段AD上运动,点E在AC上,且AE=2,当EF+CF取最小值时,∠ECF=30°.
如图,等边△ABC中,AB=4,AD⊥BC于点D,点F在线段AD上运动,点E在AC上,且AE=2,当EF+CF取最小值时,∠ECF=30°. 分析 如图,作点E关于直线AD的对称点E′,连接CE′交AD于F′.由EF+FC=FE′+FC,所以当C、E′、F共线时,EF+CF最小,由△ABC是等边三角形,AB=BC=AC=4,AE=AE′=2,推出AE′=E′B,∠ACB=60°,推出∠ACE′=∠BCE′=30°,即可解决问题.
解答 解:如图,作点E关于直线AD的对称点E′,连接CE′交AD于F′.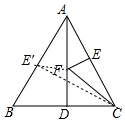
∵EF+FC=FE′+FC,
∴当C、E′、F共线时,EF+CF最小,
∵△ABC是等边三角形,AB=BC=AC=4,AE=AE′=2,
∴AE′=E′B,∠ACB=60°
∴∠ACE′=∠BCE′=30°,
∴此时∠ECF=30°,
故答案为30.
点评 本题考查轴对称、等边三角形的性质、垂线段最短等知识,解题的关键是灵活运用所学知识,学会利用对称解决最值问题,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 当m=-2时,函数图象与x轴没有交点 | |
| B. | 当m=1时,函数图象过点(-1,1) | |
| C. | 若m<0,则当x≤1时,y随x的增大而增大 | |
| D. | 若m>0,则当x≥1时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
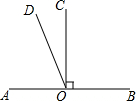 如图,已知直线AB,线段CO⊥AB于点O,∠AOD=$\frac{1}{2}$∠BOD,∠COD的度数为( )
如图,已知直线AB,线段CO⊥AB于点O,∠AOD=$\frac{1}{2}$∠BOD,∠COD的度数为( )| A. | 15° | B. | 25° | C. | 30° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
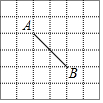 如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )
如图,在6×6的正方形网格中,点A,B均在正方形格点上,若在网格中的格点上找一点C,使△ABC为等腰三角形,这样的点C一共有( )| A. | 7个 | B. | 8个 | C. | 10个 | D. | 12个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
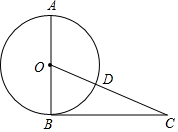 如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC相交于点D,且CD=2,BC=4,
如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC相交于点D,且CD=2,BC=4,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com