
如下图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP
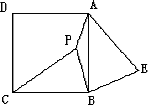
(1)在图中是否存在两个全等的三角形,若存在请写出这两个三角形并证明;若不存在请说明理由.
(2)若(1)中存在,这两个三角形通过旋转能够互相重合吗?若重合请说出旋转的过程;若不重合请说明理由.
(3)PB与BE有怎样的位置关系,说明理由.
(4)若PA=1,PB=2,∠APB=135°,求AE的值.
|
(1)存在.⊿CPB≌⊿AEB,证明如下:∵四边形ABCD是正方形,∴AB=CB,∵∠ABE=∠CBP,BE=BP∴⊿CPB≌⊿AEB. (2)重合.⊿CPB绕B点按顺时针方向旋转90°可得到⊿AEB. (3)PB⊥BE.理由如下:由(1)知:⊿CPB≌⊿AEB,∴∠ABE=∠CBP∵四边形ACBD是正方形,∴∠ABC=90°即∠CBP+∠ABP=90°,∴∠ABE+∠ABP=90°,∴PB⊥BE. (4)连接PE,∵PB=EB,∴∠BPE=∠BEP,∵∠PBE=90°,∴∠BPE=45°,∵∠APB=135°,∴∠APE=∠APB-∠BPE=90°,
在Rt⊿BPE中, 在Rt⊿APE中, |


科目:初中数学 来源: 题型:
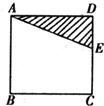 29、如下图,E是正方形ABCD中CD边上任一点,以点A为中心,把△ADE顺时针旋转90°,在给出图形中画出旋转后的图形,并完成下列填空.
29、如下图,E是正方形ABCD中CD边上任一点,以点A为中心,把△ADE顺时针旋转90°,在给出图形中画出旋转后的图形,并完成下列填空.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
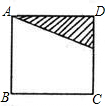 如下图,E是正方形ABCD中CD边上任一点,以点A为中心,把△ADE顺时针旋转90°,在给出图形中画出旋转后的图形,并完成下列填空.
如下图,E是正方形ABCD中CD边上任一点,以点A为中心,把△ADE顺时针旋转90°,在给出图形中画出旋转后的图形,并完成下列填空.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2008-2009学年山东省菏泽市郓城县九年级(上)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com