
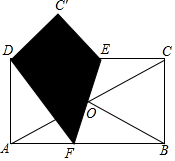
 如图是一个矩形纸片ABCD,连接AC,DB交于点O,且AC=4$\sqrt{5}$,若AD:AB=1:2,将纸片折叠使B与D重合,折痕为EF,求折叠后纸片重合部分的面积.
如图是一个矩形纸片ABCD,连接AC,DB交于点O,且AC=4$\sqrt{5}$,若AD:AB=1:2,将纸片折叠使B与D重合,折痕为EF,求折叠后纸片重合部分的面积. 分析 根据矩形的性质得到∠DAB=90°,根据勾股定理得到AD=4,AB=8,根据折叠的性质得到CE=C′E,DC′=BC=4,∠C′=∠DCB=90°,根据勾股定理得到DE=5,根据三角形的面积公式即可得到结论.
解答 解:∵四边形ABCD是矩形,
∴∠DAB=90°,
∵AD:AB=1:2,
∴设AD=x,AB=2x,
∴AC=$\sqrt{5}$x=4$\sqrt{5}$,
∴x=4,
∴AD=4,AB=8,
∵将纸片折叠使B与D重合,折痕为EF,
∴CE=C′E,DC′=BC=4,∠C′=∠DCB=90°,
∴C′D2+C′E2=DE2,即42+C′E2=(8-C′E)2,
∴C′E=3,
∴DE=5,
∴纸片重合部分的面积=$\frac{1}{2}$5×4=10.
点评 本题考查了翻折变换-折叠问题,矩形的性质,三角形面积的计算,勾股定理,熟练掌握折叠的性质是解题的关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
 已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B、C两点.
已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B、C两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
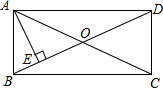 如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.
如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为2cm,分别以A为原点,AB,AD边所在的直线为坐标轴建立平面直角坐标系后,将正方形ABCD以点B为旋转中心,沿着x轴的正方向顺时针旋转90°称为第一次振动,再以点C为旋转中心沿着x轴的正方向顺时针旋转90°称为第2次滚动…,以此类推,将正方形ABCD做无滑动地滚动下去.则第2017次滚动时点A的对应点的运动路径长是(504.5+252$\sqrt{2}$)πcm.
如图,正方形ABCD的边长为2cm,分别以A为原点,AB,AD边所在的直线为坐标轴建立平面直角坐标系后,将正方形ABCD以点B为旋转中心,沿着x轴的正方向顺时针旋转90°称为第一次振动,再以点C为旋转中心沿着x轴的正方向顺时针旋转90°称为第2次滚动…,以此类推,将正方形ABCD做无滑动地滚动下去.则第2017次滚动时点A的对应点的运动路径长是(504.5+252$\sqrt{2}$)πcm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 七巧板被西方人称为“东方魔板”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图a)的边长为4,则“一帆风顺”(如图b)阴影部分的面积为1.
七巧板被西方人称为“东方魔板”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图a)的边长为4,则“一帆风顺”(如图b)阴影部分的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
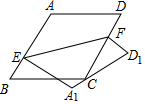 如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,$\frac{BE}{AE}$的值等于( )
如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,$\frac{BE}{AE}$的值等于( )| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}-1}{6}$ | C. | $\frac{\sqrt{3}+1}{8}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com