
【题目】已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为 .
【答案】y=x2﹣2x﹣3
【解析】解:∵y=x2+2x+1=(x+1)2,
∴A点坐标为(﹣1,0),
解方程组 ![]() 得
得 ![]() 或
或 ![]() ,
,
∴点C′的坐标为(1,4),
∵点C和点C′关于x轴对称,
∴C(1,﹣4),
设原抛物线解析式为y=a(x﹣1)2﹣4,
把A(﹣1,0)代入得4a﹣4=0,解得a=1,
∴原抛物线解析式为y=(x﹣1)2﹣4=x2﹣2x﹣3.
所以答案是y=x2﹣2x﹣3.
【考点精析】掌握二次函数的性质和抛物线与坐标轴的交点是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,直线PQ∥MN,点C是PQ、MN之间(不在直线PQ,MN上)的一个动点.

(1)若∠1与∠2都是锐角,如图甲,请直接写出∠C与∠1,∠2之间的数量关系;
(2)若把一块三角尺(∠A=30°,∠C=90°)按如图乙方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数;
(3)将图乙中的三角尺进行适当转动,如图丙,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,求![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:①0是最小的整数;②有理数不是正数就是负数;③非负数就是正数;④![]() 不仅是有理数,而且是分数;⑤
不仅是有理数,而且是分数;⑤![]() 是无限不循环小数,所以不是有理数;⑥无限小数不都是有理数;⑦正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )
是无限不循环小数,所以不是有理数;⑥无限小数不都是有理数;⑦正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )
A.7个B.6个C.5个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.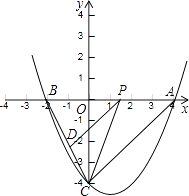
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
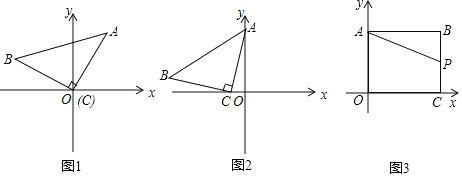
【题目】![]() 操作思考:如图1,在平面直角坐标系中,等腰
操作思考:如图1,在平面直角坐标系中,等腰![]() 的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点
的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点![]() 处
处![]() 则
则![]() 的长为______;
的长为______;![]() 点B的坐标为______
点B的坐标为______![]() 直接写结果
直接写结果![]()
![]() 感悟应用:如图2,在平面直角坐标系中,将等腰
感悟应用:如图2,在平面直角坐标系中,将等腰![]() 如图放置,直角顶点
如图放置,直角顶点![]() ,点
,点![]() ,试求直线AB的函数表达式.
,试求直线AB的函数表达式.
![]() 拓展研究:如图3,在直角坐标系中,点
拓展研究:如图3,在直角坐标系中,点![]() ,过点B作
,过点B作![]() 轴,垂足为点A,作
轴,垂足为点A,作![]() 轴,垂足为点C,P是线段BC上的一个动点,点Q是直线
轴,垂足为点C,P是线段BC上的一个动点,点Q是直线![]() 上一动点
上一动点![]() 问是否存在以点P为直角顶点的等腰
问是否存在以点P为直角顶点的等腰![]() ,若存在,请求出此时P的坐标,若不存在,请说明理由.
,若存在,请求出此时P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
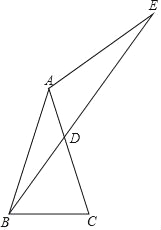
【题目】如图,已知△ABC中AB=AC,在AC上有一点D,连接BD,并延长至点E,使AE=AB.
(1)画图:作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,连接CF,求证:∠ABE=∠ACF;
(3)若AC=8,∠E=15°,求三角形ABE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com