
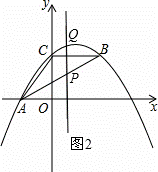
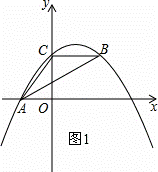
如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
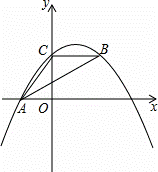
解:(1)如图1,
∵A(﹣3,0),C(0,4),
∴OA=3,OC=4.
∵∠AOC=90°,
∴AC=5.
∵BC∥AO,AB平分∠CAO,
∴∠CBA=∠BAO=∠CAB.
∴BC=AC.
∴BC=5.
∵BC∥AO,BC=5,OC=4,
∴点B的坐标为(5,4).
∵A(﹣3.0)、C(0,4)、B(5,4)在抛物线y=ax2+bx+c上,
∴
解得: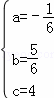
∴抛物线的解析式为y=﹣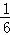 x2+
x2+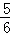 x+4.
x+4.
(2)如图2,
设直线AB的解析式为y=mx+n,
∵A(﹣3.0)、B(5,4)在直线AB上,
∴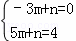
解得: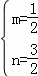
∴直线AB的解析式为y=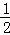 x+
x+ .
.
设点P的横坐标为t(﹣3≤t≤5),则点Q的横坐标也为t.
∴yP=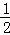 t+
t+ ,yQ=﹣
,yQ=﹣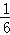 t2+
t2+ t+4.
t+4.
∴PQ=yQ﹣yP=﹣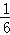 t2+
t2+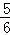 t+4﹣(
t+4﹣(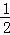 t+
t+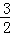 )
)
=﹣ t2+
t2+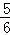 t+4﹣
t+4﹣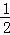 t﹣
t﹣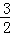
=﹣ t2+
t2+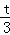 +
+
=﹣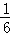 (t2﹣2t﹣15)
(t2﹣2t﹣15)
=﹣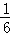 [(t﹣1)2﹣16]
[(t﹣1)2﹣16]
=﹣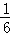 (t﹣1)2+
(t﹣1)2+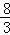 .
.
∵﹣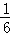 <0,﹣3≤1≤5,
<0,﹣3≤1≤5,
∴当t=1时,PQ取到最大值,最大值为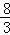 .
.
∴线段PQ的最大值为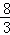 .
.
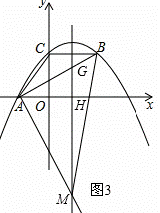
(3)①当∠BAM=90°时,如图3所示.
抛物线的对称轴为x=﹣ =﹣
=﹣ =
=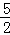 .
.
∴xH=xG=xM=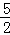 .
.
∴yG= ×
×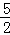 +
+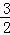 =
=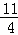 .
.
∴GH=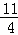 .
.
∵∠GHA=∠GAM=90°,
∴∠MAH=90°﹣∠GAH=∠AGM.
∵∠AHG=∠MHA=90°,∠MAH=∠AGM,
∴△AHG∽△MHA.
∴ .
.
∴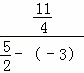 =
=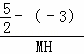 .
.
解得:MH=11.
∴点M的坐标为(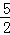 ,﹣11).
,﹣11).
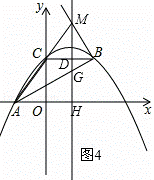
②当∠ABM=90°时,如图4所示.
∵∠BDG=90°,BD=5﹣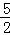 =
=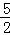 ,DG=4﹣
,DG=4﹣ =
=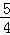 ,
,
∴BG=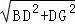
=
= .
.
同理:AG= .
.
∵∠AGH=∠MGB,∠AHG=∠MBG=90°,
∴△AGH∽△MGB.
∴ =
=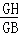 .
.
∴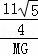 =
=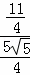 .
.
解得:MG=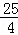 .
.
∴MH=MG+GH
=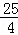 +
+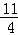
=9.
∴点M的坐标为(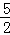 ,9).
,9).
综上所述:符合要求的点M的坐标为(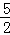 ,9)和(
,9)和(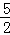 ,﹣11).
,﹣11).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
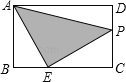
如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com