
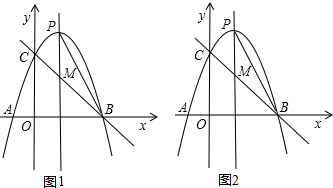
���� ��1����A��-1��0����B��3��0���������y=-x2+bx+c��������������ߵĽ���ʽ��
��2����D������Ϊ��t��-t2+2t+3��������D��DH��x����H������S��BCD=S����OCDH+S��BDH-S��BOC�T-$\frac{3}{2}$t2+$\frac{9}{2}$t���������䷽���������D�����꼰��BCD��������ֵ��
��3����PM��x�ύ�ڵ�E���������E��BCƽ�е�ֱ��EQ����ʽΪy=-x+1���ⷽ����$\left\{\begin{array}{l}{y=-x+1}\\{y=-{x}^{2}+2x+3}\end{array}\right.$�����ɵó���Q�����꣮
��� �⣺��1����������y=-x2+bx+c��x�ύ�ڵ�A��-1��0����B��3��0����
��$\left\{\begin{array}{l}{-1+b+c=0}\\{-9+3b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$��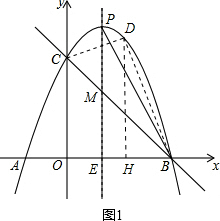 �������ߵĽ���ʽΪy=-x2+2x+3��
�������ߵĽ���ʽΪy=-x2+2x+3��
��2����ͼ1����D������Ϊ��t��-t2+2t+3��������D��DH��x����H��
��S��BCD=S����OCDH+S��BDH-S��BOC
=$\frac{1}{2}$��-t2+2t+3+3��t+$\frac{1}{2}$��3-t����-t2+2t+3��-$\frac{1}{2}$��3��3
=-$\frac{3}{2}$t2+$\frac{9}{2}$t
=-$\frac{3}{2}$��t-$\frac{3}{2}$��2+$\frac{27}{8}$��
��-$\frac{3}{2}$��0��
�൱t=$\frac{3}{2}$ʱ��D�������ǣ�$\frac{3}{2}$��$\frac{15}{4}$������BCD��������ֵ��$\frac{27}{8}$��
��3����ͼ2����PM��x�ύ�ڵ�E��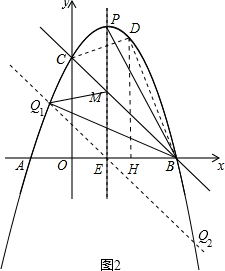 ��y=-x2+2x+3=-��x-1��2+4��
��y=-x2+2x+3=-��x-1��2+4��
��P���������1��4����E���������1��0����
��B��3��0����C��0��3����
��ֱ��BC�Ľ���ʽΪy=-x+3��
�൱x=1ʱ��y=2��
��M���������1��2����
��PM=ME=2��BMΪ��BPE�����ߣ�
��S��PMB=S��EMB��
��E��BC��ƽ���ߣ����������ڵ�Q����S��QMB=S��EMB��
��S��QMB=S��PMB��
��E��1��0����ֱ��BC�Ľ���ʽΪy=-x+3��EQ��BC��
��ֱ��EQ�Ľ���ʽΪy=-x+1��
��$\left\{\begin{array}{l}{y=-x+1}\\{y=-{x}^{2}+2x+3}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=\frac{3-\sqrt{17}}{2}}\\{y=\frac{\sqrt{17}-1}{2}}\end{array}\right.$����$\left\{\begin{array}{l}{x=\frac{3+\sqrt{17}}{2}}\\{y=-\frac{1+\sqrt{17}}{2}}\end{array}\right.$��
���Q������ΪQ1��$\frac{3-\sqrt{17}}{2}$��$\frac{\sqrt{17}-1}{2}$����Q2��$\frac{3+\sqrt{17}}{2}$��-$\frac{1+\sqrt{17}}{2}$����
����ֱ��BC�·����������ϴ��ڵ�Q��ʹ�á�QMB���PMB�������ȣ���ʱ��Q������ΪQ1��$\frac{3-\sqrt{17}}{2}$��$\frac{\sqrt{17}-1}{2}$����Q2��$\frac{3+\sqrt{17}}{2}$��-$\frac{1+\sqrt{17}}{2}$����
���� �����Ƕ��κ����ۺ��⣬�����˴���ϵ��������κ�����һ�κ����Ľ���ʽ�����κ�����ͼ�������ʣ������Ρ����ε����������ʽƽ�ƵĹ��ɣ�ֱ���������ߵĽ����������Ѷ����У�����Ĺؼ��ǣ���1�����ô���ϵ����������κ�������ʽ����2����D������Ϊ��t��-t2+2t+3�������ø�����S��BCD����t�Ķ��κ�������ʽ����3���ҵ�Q��λ�ã����ֱ��EQ�Ľ���ʽ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-4=��x+4����x-4�� | B�� | x2-2x-15=��x+3����x-5�� | C�� | 3mx-6my=3m��x-6y�� | D�� | 2x+4=2��x+4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��3 | B�� | x��3 | C�� | x��-3 | D�� | x��0 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com