[题目]过四边形的一个顶点可以画一条对角线.且把四边形分成两个三角形,过五边形的一个顶点可以画两条对角线.且把五边形分成三个三角形,......猜想:过n边形的一个顶点可以画条对角线.且把n边形分成个三角形．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】过四边形的一个顶点可以画一条对角线，且把四边形分成两个三角形；过五边形的一个顶点可以画两条对角线，且把五边形分成三个三角形；......猜想：过n边形的一个顶点可以画_________条对角线，且把n边形分成 _________个三角形．

【答案】

【解析】

根据四边形可以条对角线，被分成了4-2=2个三角形，五边形可以引条对角线，被分成了5-2=3个三角形，依此类推，n边形可以引条对角线，被分成个三角形．

从四边形的一个顶点出发，可以引1条对角线，将四边形分成2个三角形；从五边形的一个顶点出发，可以引2条对角线，将五边形分成3个三角形；从六边形的一个顶点出发，可以引3条对角线，将六边形分成4个三角形；从n边形的一个顶点出发，可以引条对角线，将n边形分成个三角形

故答案为：，．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在锐角△ABC中，AB=4，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是__________．

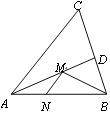
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图,∠B、∠D的两边分别平行.

(1)在图1中, ∠B与∠D的数量关系是；

(2)在图2中, ∠B与∠D的数量关系是；

(3)用一句话归纳的结论为

(4)应用:若两个角的两边分别互相平行,其中一个角比另一个角的2倍小30°,求着两个角的度数.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在四张背面完全相同的纸牌A、B、C、D，其中正面分别画有四个不同的几何图形（如图），小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸一张．

（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌可用A、B、C、D表示）；
（2）求摸出两张纸牌牌面上所画几何图形，既是轴对称图形又是中心对称图形的概率．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，轮船甲位于码头O的正西方向A处，轮船乙位于码头O的正北方向C处，某一时刻，AC＝18km，且OA＝OC．轮船甲自西向东匀速行驶，同时轮船乙沿正北方向匀速行驶，它们的速度分别为40km/h和30km/h，经过0.2h，轮船甲行驶至B处，轮船乙行驶至D处，求此时B处距离D处多远？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（1）如图①∠1＋∠2与∠B＋∠C有什么关系？为什么？

（2）把图①△ABC沿DE折叠，得到图②，填空：∠1＋∠2_______∠B＋∠C(填“＞”“＜”“=”)，当∠A＝40°时，∠B＋∠C＋∠1＋∠2＝______.

（3）如图③,是由图①的△ABC沿DE折叠得到的,如果∠A＝30°,则x＋y＝360°－（∠B＋∠C＋∠1＋∠2）＝360°－＝ ,猜想∠BDA＋∠CEA与∠A的关系为

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读理解：已知点P（x0 ， y0）和直线y=kx+b，则点P到直线y=kx+b的距离，可用公式d= 计算．
例如：求点P（﹣1，2）到直线y=3x+7的距离．
解：因为直线y=3x+7，其中k=3，b=7．
所以点P（﹣1，2）到直线y=3x+7的距离为：d= = = = ．
根据以上材料，解答下列问题：
（1）求点P（1，﹣1）到直线y=x﹣1的距离；
（2）已知⊙Q的圆心Q坐标为（0，5），半径r为2，判断⊙Q与直线y= x+9的位置关系并说明理由；
（3）已知直线y=﹣2x+4与y=﹣2x﹣6平行，求这两条直线之间的距离．