
 的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,
的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,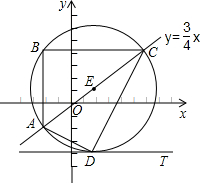 再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.
再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D. 的图象上;
的图象上; x得,
x得, (a+8)=
(a+8)= a+6,
a+6, x上,
x上, ,所以y=b+6,
,所以y=b+6, x的图象上.
x的图象上.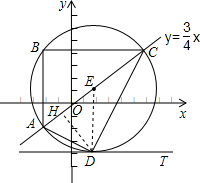
 =10,
=10, AC=5,
AC=5,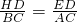 ,
,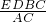 =
=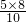 =4,
=4, ×10×4=20(平方单位).
×10×4=20(平方单位).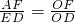 ,
,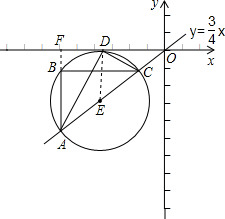
 x,OD=x+4,
x,OD=x+4,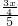 =
= ,
, ,
, x=
x= ×
× =2,
=2, ,2),
,2), ,-8).
,-8). ,2)、A2(-
,2)、A2(- ,-8).
,-8). x中,我们发现得出的值,同A的横坐标代入后得出的值是相同的.因此C点在直线y=
x中,我们发现得出的值,同A的横坐标代入后得出的值是相同的.因此C点在直线y= x上.
x上.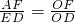


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2006-2007年福建省福州市九年级第一学期期末考试数学卷 题型:解答题
(本题满分14分)
如图,将一次函数 的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.
的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.
【小题1】(1) 求证:点C在一次函数 的图象上;
的图象上;
【小题2】(2) 求三角形ADC的面积;
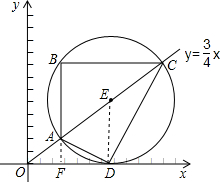
【小题3】(3) 当点D在x轴上时,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源:2006-2007年福建省福州市九年级第一学期期末考试数学卷 题型:解答题
(本题满分14分)
如图,将一次函数 的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.
的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.

1.(1) 求证:点C在一次函数 的图象上;
的图象上;
2.(2) 求三角形ADC的面积;
3.(3) 当点D在x轴上时,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源:2006-2007学年福建省福州市九年级(上)期末数学试卷(解析版) 题型:解答题
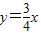 的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.
的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.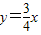 的图象上;
的图象上;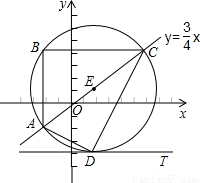
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分14分)
如图,将一次函数![]() 的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.
的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.
1.(1) 求证:点C在一次函数![]() 的图象上;
的图象上;
2.(2) 求三角形ADC的面积;
3.(3) 当点D在x轴上时,求点A的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com