
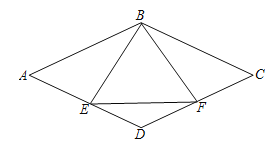
【题目】如图,点E、F分别为菱形ABCD边AD、CD的中点.
(1)求证:BE=BF;
(2)当△BEF为等边三角形时,求证:∠D=2∠A.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)根据菱形的性质得到AB=CB,AD=CD,∠A=∠C,再根据中点的定义得到AE=CF,根据SAS可证△BAE≌△BCF,根据全等三角形的性质得到BE=BF即可;
(2)作辅助线,先根据线段垂直平分线的逆定理证明BD是EF的垂直平分线,由等边三角形三线合一得:EG=FG,∠EBG=![]() ∠EBF=30°,设EG=x,则BE=2x,BG=
∠EBF=30°,设EG=x,则BE=2x,BG=![]() x,根据中位线定理得:AO=2EG=2x,OB=
x,根据中位线定理得:AO=2EG=2x,OB=![]() x,证明△BHO∽△BEG,列比例式可得OH=
x,证明△BHO∽△BEG,列比例式可得OH= ![]() ,BH=
,BH=![]() x,再求AH=
x,再求AH=![]() x,则AH=BH,可得∠DAB=60°,∠ADC=120°,从而得出结论.
x,则AH=BH,可得∠DAB=60°,∠ADC=120°,从而得出结论.
试题解析:证明:(1)∵四边形ABCD是菱形,∴∠A=∠C,AB=BC=AD=CD.∵点E、F分别为菱形ABCD边AD、CD的中点,∴AE=![]() AD,CF=
AD,CF=![]() CD,∴AE=CF,∴△ABE≌△CBF(SAS),∴BE=BF;
CD,∴AE=CF,∴△ABE≌△CBF(SAS),∴BE=BF;
(2)如图,连接AC、BD交于点O,设BD与EF交于G,AC与BE交于H,则AC⊥BD.∵BE=BF,ED=DF,∴BD是EF的垂直平分线,∴EG=FG,∠EBG=![]() ∠EBF=30°,Rt△BEG中,设EG=x,则BE=2x,BG=
∠EBF=30°,Rt△BEG中,设EG=x,则BE=2x,BG=![]() x.∵EG∥AO,E为AD的中点,∴G是OD的中点,∴AO=2EG=2x,OB=
x.∵EG∥AO,E为AD的中点,∴G是OD的中点,∴AO=2EG=2x,OB=![]() x.∵OH∥GE,∴△BHO∽△BEG,∴
x.∵OH∥GE,∴△BHO∽△BEG,∴![]() ,∴
,∴![]() =
=![]() =
=![]() ,∴OH=
,∴OH= ![]() ,BH=
,BH=![]() x,∴AH=AO﹣OH=2x﹣
x,∴AH=AO﹣OH=2x﹣![]() x=
x=![]() x,∴AH=BH,∴∠HAB=∠ABH.∵∠BHC=∠HAB+∠ABH=60°,∴∠HAB=30°,∴∠DAB=60°,∴∠ADC=120°,∴∠ADC=2∠DAB,即∠D=2∠A.
x,∴AH=BH,∴∠HAB=∠ABH.∵∠BHC=∠HAB+∠ABH=60°,∴∠HAB=30°,∴∠DAB=60°,∴∠ADC=120°,∴∠ADC=2∠DAB,即∠D=2∠A.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图是一个汉字“互”字,其中,AB∥CD,∠1=∠2,∠MGH=∠MEF.

求证:∠MEF=∠GHN.
证明:∵ AB∥CD(已知)
∴∠1=∠3( )
又∵∠1=∠2(已知)
∴∠2=∠3( )
∴ME∥HN ( )
∴∠MGH=∠ ( )( )
又∵∠MGH=∠MEF (已知)
∴∠MEF=∠GHN( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有两点A、B,点B在点A的右侧,且AB=10,点A表示的数为﹣6.动点P从点A出发,以每秒4个单位长度的速度沿数轴向右匀速运动.
(1)写出数轴上点B表示的数;
(2)经过多少时间,线段AP和BP的长度之和为18?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
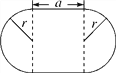
【题目】一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长l;
(2)花坛的面积S;
(3)若a=8m,r=5m,求此时花坛的周长及面积(π取3.14).
查看答案和解析>>
科目:初中数学 来源: 题型:
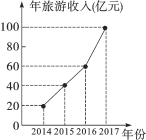
【题目】某人为了解他所在地区的旅游情况,收集了该地区2014年到2017年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题:
(1)该地区2014年到2017年四年的年旅游平均收入是多少亿元;
(2)从折线统计图中你能获得哪些信息?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学开展4种课外兴趣小组活动,分别为A;绘画:B;机器人:C;跳舞:D;吉他.每个学生都要选取一个兴趣小组参与活动,小明对同学们选取的活动形式进行了随机抽样调查,根据调查统计结果,绘制了如下的统计图:
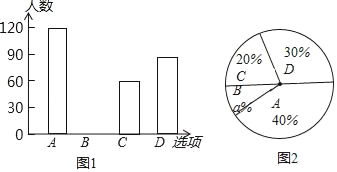
(1)本次调查学生共 人,a= ,并将条形图补充完整;
(2)如果该校有学生500人,则选择“机器人”活动的学生估计有多少人?
(3)学校让每班同学在A,B,C,D四种活动形式中,随机抽取两种开展活动,请用树状图或列表法的方法,求每班抽取的两种形式恰好是“绘画”和“机器人”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.

(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,同学们遇到这样一个问题:
如图1,已知![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 与
与 ![]() 的角平分线,请同学们根据题中的条件提出问题,大家一起来解决(本题出现的角均小于平角)
的角平分线,请同学们根据题中的条件提出问题,大家一起来解决(本题出现的角均小于平角)
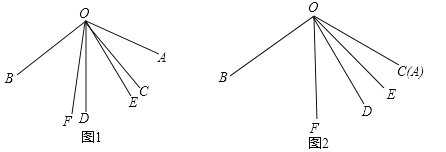
同学们经过思考后,交流了自己的想法:
小强说:“如图2,若![]() 与
与![]() 重合,且
重合,且![]() ,
,![]() 时,可求
时,可求![]() 的度数.”
的度数.”
小伟说:“在小强提出问題的前提条件下,将![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 逆时针
逆时针
转动![]() ,可求出
,可求出![]() 的值.”
的值.”
老师说:“在原題的条件下,借助射线![]() 的不同位置可得出的数量关系.”
的不同位置可得出的数量关系.”
(1)请解决小强提出的问题;
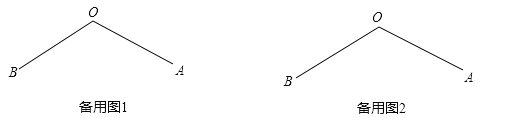
(2)在备用图1中,补充完整的图形,并解决小伟提出的问题
(3)在备用图2中,补充完整的图形,并解决老师提出的问题,即求![]() 三者之间的的数量关系.
三者之间的的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com