
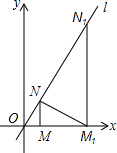
 如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M30的坐标为(261,0).
如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M30的坐标为(261,0). 分析 根据直线l的解析式求出∠MON=60°,从而得到∠MNO=∠OM1N=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出OM1=22•OM,然后表示出OMn与OM的关系,再根据点Mn在x轴上写出坐标即可写出M30的坐标.
解答  解:如图,∵直线l:y=$\sqrt{3}$x,
解:如图,∵直线l:y=$\sqrt{3}$x,
∴∠MON=60°,
∵NM⊥x轴,M1N⊥直线l,
∴∠MNO=∠OM1N=90°-60°=30°,
∴ON=2OM,OM1=2ON=4OM=22•OM,
同理,OM2=22•OM1=(22)2•OM,
…,
OMn=(22)n•OM=22n•2=22n+1,
所以,点Mn的坐标为(22n+1,0).
所以,点M30的坐标为(261,0).
故答案为:(261,0).
点评 本题考查了一次函数图象上点的坐标特征,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质并求出变化规律是解题的关键.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
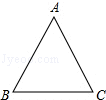 如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$
如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 4-2$\sqrt{3}$ | B. | 2$\sqrt{3}$-4 | C. | -$\frac{2}{3}\sqrt{3}$ | D. | $\frac{2}{3}\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
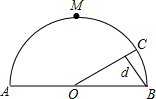 如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是( )
如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是( )| A. | 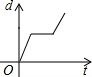 | B. | 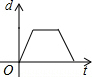 | C. | 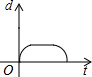 | D. | 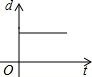 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
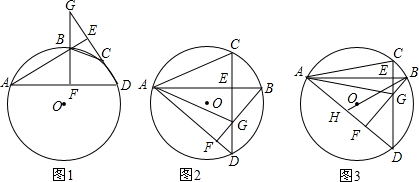
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 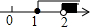 | B. | 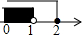 | C. | 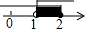 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这组数据的平均数是75 | B. | 这组数据的中位数是74 | ||
| C. | 这组数据的方差是3.2 | D. | 这组数据的众数是76 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com