
【题目】如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=![]() 和y=
和y=![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①![]() ;②阴影部分面积是
;②阴影部分面积是![]() (k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )
(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )

A.①②B.①④C.③④D.①②③
【答案】B
【解析】
作AE⊥y轴于点E,CF⊥y轴于点F,根据平行四边形的性质得S△AOB=S△COB,利用三角形面积公式得到AE=CF,则有OM=ON,再利用反比例函数k的几何意义和三角形面积公式得到S△AOM=![]() |k1|=
|k1|=![]() OMAM,S△CON=
OMAM,S△CON=![]() |k2|=
|k2|=![]() ONCN,所以有
ONCN,所以有![]() ;由S△AOM=
;由S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|,得到S阴影部分=S△AOM+S△CON=
|k2|,得到S阴影部分=S△AOM+S△CON=![]() (|k1|+|k2|)=
(|k1|+|k2|)=![]() (k1-k2);当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.
(k1-k2);当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.
作AE⊥y轴于E,CF⊥y轴于F,如图,
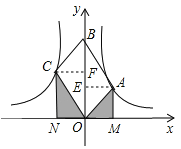
∵四边形OABC是平行四边形,
∴S△AOB=S△COB,
∴AE=CF,
∴OM=ON,
∵S△AOM=![]() |k1|=
|k1|=![]() OMAM,S△CON=
OMAM,S△CON=![]() |k2|=
|k2|=![]() ONCN,
ONCN,
∴![]() ,故①正确;
,故①正确;
∵S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|
|k2|
∴S阴影部分=S△AOM+S△CON=![]() (|k1|+|k2|),
(|k1|+|k2|),
而k1>0,k2<0,
∴S阴影部分=![]() (k1-k2),故②错误;
(k1-k2),故②错误;
当∠AOC=90°,
∴四边形OABC是矩形,
∴不能确定OA与OC相等,
而OM=ON,
∴不能判断△AOM≌△CNO,
∴不能判断AM=CN,
∴不能确定|k1|=|k2|,故③错误;
若OABC是菱形,则OA=OC,
而OM=ON,
∴Rt△AOM≌Rt△CNO,
∴AM=CN,
∴|k1|=|k2|,
∴k1=-k2,
∴两双曲线既关于x轴对称,也关于y轴对称,故④正确.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,正![]() 内接于
内接于![]() 是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() 图中共有6对相似三角形.
图中共有6对相似三角形.
其中,正确结论的个数为![]()
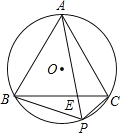
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差 (单位:千克) |
|
|
| 1 | 2 |
箱数 | 2 | 6 | 10 | 8 | 4 |
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为一幅重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() 与x轴、y轴分别相交于点A和点B,点C在线段AO上.将
与x轴、y轴分别相交于点A和点B,点C在线段AO上.将![]() 沿BC折叠后,点O恰好落在AB边上点D处.
沿BC折叠后,点O恰好落在AB边上点D处.
(1)求出OC的长?
(2)点E、F是直线BC上的两点,若![]() 是以EF为斜边的等腰直角三角形,求点F的坐标;
是以EF为斜边的等腰直角三角形,求点F的坐标;
(3)取AB的中点M,若点P在y轴上,点Q在直线AB上,是否存在以C、M、P、Q为顶点的四边形为平行四边形?若存在,请求出所有满足条件的Q点坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)直接写出:以A、B、C为顶点的平形四边形的第四个顶点D的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年,随州学子尤东梅参加《最强大脑》节目,成功完成了高难度的项目挑战,展现了惊人的记忆力.在2019年的《最强大脑》节目中,也有很多具有挑战性的比赛项目,其中《幻圆》这个项目充分体现了数学的魅力.如图是一个最简单的二阶幻圆的模型,要求:①内、外两个圆周上的四个数字之和相等;②外圆两直径上的四个数字之和相等,则图中两空白圆圈内应填写的数字从左到右依次为______和______.
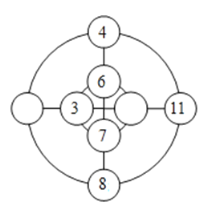
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
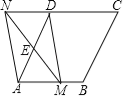
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com