
分析 先通分,再把分子相加减,最后把x的值代入进行计算即可.
解答 解:原式=$\frac{(x+1)^{2}-4x}{(x+1)(x-1)}$
=$\frac{{x}^{2}+2x+1-4x}{(x+1)(x-1)}$
=$\frac{{x}^{2}+1-2x}{(x+1)(x-1)}$
=$\frac{{(x-1)}^{2}}{(x+1)(x-1)}$
=$\frac{x-1}{x+1}$,
当x=$\sqrt{2}$-1时,原式=$\frac{\sqrt{2}-1-1}{\sqrt{2}-1+1}$=$\frac{\sqrt{2}-2}{\sqrt{2}}$=1-$\sqrt{2}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


科目:初中数学 来源: 题型:解答题
| 干家务活平均时间 | 频数 | 百分比 |
| A(0-10min) | 10 | 25% |
| B(11-20min) | a | 62.5% |
| C(21-30min) | 5 | b |
| 合 计 | c | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 23000名考生的成绩是总体 | |
| B. | 每名考生是个体 | |
| C. | 200名考生的成绩是总体的一个样本 | |
| D. | 每名考生的成绩是个体 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
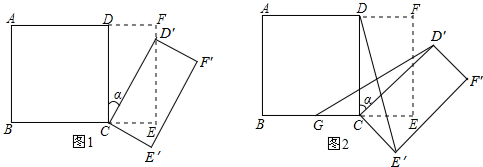
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com