
 在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,-1),B(3,-1),动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.过P作PQ⊥OA于Q.设P点运动的时间为t秒(0<t<2),△OPQ与四边形OABC重叠的面积为S.
在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,-1),B(3,-1),动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.过P作PQ⊥OA于Q.设P点运动的时间为t秒(0<t<2),△OPQ与四边形OABC重叠的面积为S.分析 (1)利用对称性得到抛物线与x轴的另一个交点坐标为(4,0),则设交点式y=ax(x-4),然后把A点坐标代入求出a即可得到抛物线的解析式,再利用配方法得到顶点M的坐标;
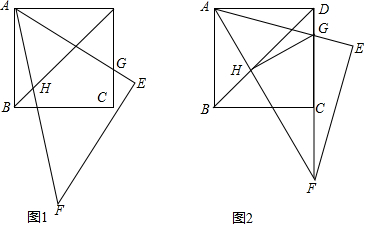
(2)作QN⊥x轴于N,AH⊥x轴于H,如图1,先判定△AOH和△ONQ为等腰直角三角形得到QN=ON=NP=$\frac{1}{2}$OP=t,然后用t表示出P点和Q点坐标;
(3)△OPQ绕P点逆时针旋转90°得到△O′PQ′,如图2,作Q′K⊥x轴于K,利用旋转的性质得∠QPQ′=90°,PO′⊥x轴,PO′=PO=2t,PQ′=PQ=$\sqrt{2}$t,再确定O′(2t,-2t),Q′(3t,-t),然后分别把O′(2t,-2t)或Q′(3t,-t)代入抛物线解析式可求出对应的t的值;
(4)根据△OPQ与四边形OABC重叠部分的图形不同分类讨论:当0<t≤1时,重叠部分为三角形,如图1,利用三角形面积公式表示出S;当1<t≤$\frac{3}{2}$时,如图3,PQ交AB于E点,重叠部分为梯形,利用三角形面积的差表示S;当$\frac{3}{2}$<t≤2,如图4,PQ交AB于E点,交BC于F点,重叠部分为梯形OABC减去△BEF,则利用梯形的面积减去三角形面积可表示出S.
解答 解:(1)∵抛物线过点A(1,-1),B(3,-1),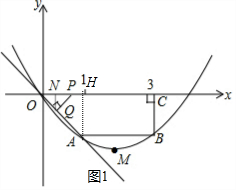
∴抛物线的对称轴为直线x=2,
∴抛物线与x轴的另一个交点坐标为(4,0),
设抛物线的解析式为y=ax(x-4),
把A(1,-1)代入得a•1•(-3)=-1,解得a=$\frac{1}{3}$,
∴抛物线的解析式为y=$\frac{1}{3}$x(x-4),即y=$\frac{1}{3}$x2-$\frac{4}{3}$x;
∵y=$\frac{1}{3}$(x-2)2-$\frac{4}{3}$,
∴顶点M的坐标为(2,-$\frac{4}{3}$);
(2)作QN⊥x轴于N,AH⊥x轴于H,如图1,
∵A(-1,1),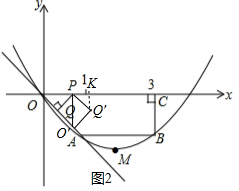
∴OH=AH=1,
∴△AOH为等腰直角三角形,
∴△ONQ为等腰直角三角形,
∴QN=ON=NP=$\frac{1}{2}$OP=t,
∴P(2t,0),Q(t,-t);
(3)存在.
△OPQ绕P点逆时针旋转90°得到△O′PQ′,如图2,作Q′K⊥x轴于K,
∠QPQ′=90°,PO′⊥x轴,PO′=PO=2t,PQ′=PQ=$\sqrt{2}$t,则O′(2t,-2t);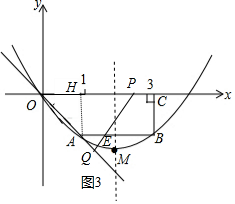
∵∠KPQ′=90°-∠OPQ=45°,
∵△PQ′K为等腰三角形,
∴PK=Q′k=t,
∴Q′(3t,-t),
当O′(2t,-2t)落在抛物线上时,-2t=$\frac{1}{3}$•4t2-$\frac{4}{3}$•2t,解得t1=0,t2=$\frac{1}{2}$;
当Q′(3t,-t)落在抛物线上时,-t=$\frac{1}{3}$•9t2-$\frac{4}{3}$•3t,解得t1=0,t2=1;
综上所述,当t为$\frac{1}{2}$或1时,使得△OPQ的顶点O或Q落在抛物线上;
(4)当0<t≤1时,如图1,S=$\frac{1}{2}$•t•2t=t;
当1<t≤$\frac{3}{2}$时,如图3,PQ交AB于E点,S=S△POQ-S△AEQ=$\frac{1}{2}$•t•2t-$\frac{1}{2}$•(t-1)•2(t-1)=2t-1;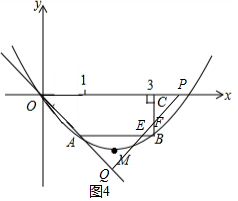
当$\frac{3}{2}$<t≤2,如图4,PQ交AB于E点,交BC于F点,
∵△POQ为等腰直角三角形,
∴∠CPF=45°,
∴△PCF为等腰直角三角形,
∴PC=CF=2t-3,
∴BF=1-(2t-3)=4-2t,
∴S△BEF=$\frac{1}{2}$(4-2t)2=2t2-8t+8,
∴S=S梯形OABC-S△BEF=$\frac{1}{2}$•(2+3)•1-(2t2-8t+8)=-2t2+8t-$\frac{11}{2}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰直角三角形的判定与性质;会利用待定系数法法求二次函数的解析式;理解坐标与图形性质.


科目:初中数学 来源: 题型:解答题
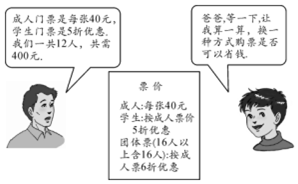 在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )| A. | $\sqrt{17}$ | B. | 6 | C. | $\sqrt{26}$ | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2×103 | B. | 2×104 | C. | 20×103 | D. | 0.2×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0 | B. | a<0 | C. | a>-$\frac{1}{2}$ | D. | a<-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>$\frac{4}{5}$ | B. | x≥8 | C. | $\frac{4}{5}$<x≤8 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 型号 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 数量(双) | 2 | 6 | 11 | 15 | 7 | 3 | 4 |
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{2017}}{2017}$ | B. | $\sqrt{2017}$ | C. | -$\sqrt{2017}$ | D. | -2017 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com