
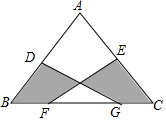
 如图,在△ABC中,AB=AC=10,BC=12,D、E分别为AB,AC中点,F、G为线段BC上两点,且FG=6,则阴影部分面积为24.
如图,在△ABC中,AB=AC=10,BC=12,D、E分别为AB,AC中点,F、G为线段BC上两点,且FG=6,则阴影部分面积为24. 分析 由勾股定理求出BC上的高AH为8,求出FG=DE FG∥DE,求出FG与DE间的距离是4,求出△FGO和△DEO的高均为2,求出阴影部分面积即可.
解答 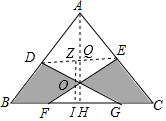 解:连接DE,过A作AH⊥BC于H,过O作ZI⊥BC于I,交DE于Z,
解:连接DE,过A作AH⊥BC于H,过O作ZI⊥BC于I,交DE于Z,
∵AB=AC=10cm,AH⊥BC,BC=12,
∴BH=CH=6,
∵AB=AC=10,
由勾股定理得:AH=8,
∵D、E分别是AB和AC中点,
∴DE=$\frac{1}{2}$BC=6,DE∥BC,
∴DE和FG间的距离是4,
∵FG=6,BC=12,
∴FG=DE,FG∥DE,
∴∠DEO=∠GFO,
在△DEO和△GFO中,
$\left\{\begin{array}{l}{∠DEO=∠GFO}\\{∠DOE=∠GOF}\\{DE=FG}\end{array}\right.$,
∴△DEO≌△GFO(AAS),
∴DO=GO,
∵DE∥FG,
∴△DZO∽△GIO,
∴$\frac{DO}{GO}$=$\frac{ZO}{IO}$,
∵DO=GO,
∴ZO=IO=$\frac{1}{2}$ZI=2,
∴阴影部分的面积是:
S梯形DECB-S△DOE-S△OFG
=$\frac{1}{2}$×(DE+BC)×IZ-$\frac{1}{2}$×DE×OZ-$\frac{1}{2}$×FG×OI
=$\frac{1}{2}$×(6+12)×4-$\frac{1}{2}$×6×2-$\frac{1}{2}$×6×2
=24.
故答案为:24.
点评 本题考查了相似三角形的性质和判定,三角形的面积,等腰三角形的性质,勾股定理,三角形的中位线定理等知识点的综合运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 到C地 | 到D地 | |
| A果园 | 每吨15元 | 每吨12元 |
| B果园 | 每吨10元 | 每吨9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
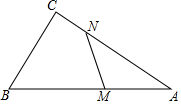 已知,在△ACB中,BC=9,AC=12,AB=15.若线段AB上有一点动点M,线段AC上有一动点N,始终保持AM=CN,若△AMN是直角三角形,且MN=4,则AM的长为$\frac{16}{3}$.
已知,在△ACB中,BC=9,AC=12,AB=15.若线段AB上有一点动点M,线段AC上有一动点N,始终保持AM=CN,若△AMN是直角三角形,且MN=4,则AM的长为$\frac{16}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
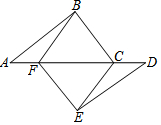 如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.
如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com