
【题目】直线MN与x轴、y轴分别交于点M、N,并且经过第二、三、四象限,与反比例函数y=![]() (k<0)的图象交于点A、B,过A、B两点分别向x轴、y轴作垂线,垂足为C、D、E、F,AD与BF交于G点.
(k<0)的图象交于点A、B,过A、B两点分别向x轴、y轴作垂线,垂足为C、D、E、F,AD与BF交于G点.
(1)比较大小:S矩形ACOD S矩形BEOF(填“>,=,<”).
(2)求证:①AGGE=BFBG;
②AM=BN;
(3)若直线AB的解析式为y=﹣2x﹣2,且AB=3MN,则k的值为 .
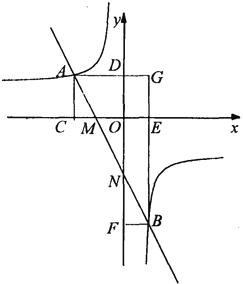
【答案】(1)=;(2)①见解析,②见解析;(3)﹣4.
【解析】
(1)根据反比例函数的比例系数的几何意义即可作出判断;
(2)①设A的横坐标是a,B的横坐标是b,分别代入y=![]() ,则A的坐标是(a,
,则A的坐标是(a,![]() ),B的坐标是(b,
),B的坐标是(b,![]() ),利用a、b表示出AG、GE、BF、BG的长,即可证得;
),利用a、b表示出AG、GE、BF、BG的长,即可证得;
②求得直线AB的解析式,即可求得M的坐标,即可证明CM=BF,即可证得△ACM≌△NFB,根据全等三角形的对应边相等,即可证得;
(3)根据AM=BN,且AB=3MN,可以得到AM=BN=MN,则OF=2ON,OM=BF,在y=﹣2x﹣2中,求得M、N的坐标,即可求得B的坐标,代入反比例函数解析式即可求得k的值.
(1)根据反比例函数k的几何意义可得:S矩形ACOD=S矩形BEOF=|k|,
故答案为:=;
(2)①设A的横坐标是a,B的横坐标是b,分别代入y=![]() ,则A的坐标是(a,
,则A的坐标是(a,![]() ),B的坐标是(b,
),B的坐标是(b,![]() ),
),
则AG=b﹣a,GE=![]() ,BF=b,BG=
,BF=b,BG=![]() ﹣
﹣![]() ,
,
则AGGE=(b﹣a)![]() =
=![]() ,
,
BFBG=b(![]() ﹣
﹣![]() )=
)=![]() ,
,
∴AGGE=BFBG;
②设过A、B的直线的解析式是y=mx+n,则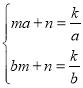 ,
,
解得: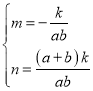 ,
,
则函数的解析式是:y=﹣![]() x+
x+![]() ,
,
令y=0,解得:x=a+b,
则M的横坐标是a+b,
∴CM=a+b﹣a=b,
∴CM=BF,
则△ACM≌△NFB,
∴AM=BN;
(3)∵AM=BN,且AB=3MN,
∴AM=BN=MN,
∴ON=NF,
在y=﹣2x﹣2中,令x=0,解得:y=﹣2,
则ON=2,
令y=0,解得:x=﹣1,则OM=1,
∴OF=2ON=4,OM=BF=1
∴B的坐标是(1,﹣4),
把(1,﹣4)代入y=![]() 中,得:k=﹣4,
中,得:k=﹣4,
故答案为:﹣4.


科目:初中数学 来源: 题型:
【题目】定义运算a![]() b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,则(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,则a=0.
b=0,则a=0.
其中正确结论的序号是 (填上你认为所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是平行四边形;
(2)如图2,连接CE,在不添加任何辅助线的情况下,请直接写出图2中所有与△BDE面积相等的三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “明天降雨的概率是60%”表示明天有60%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的概率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的概率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
![]()
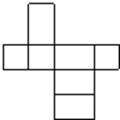
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的容积: _________ cm3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,….则顶点M2014的坐标为_______.
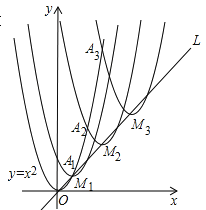
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com