
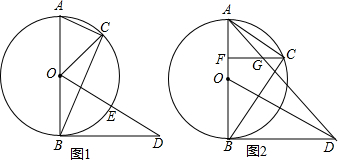
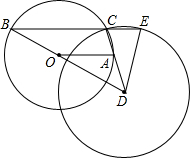 如图,在⊙O中,半径OA长为1,弦BC∥OA,射线BO,射线CA交于点D,以点D为圆心,CD为半径的⊙D交BC延长线于点E.
如图,在⊙O中,半径OA长为1,弦BC∥OA,射线BO,射线CA交于点D,以点D为圆心,CD为半径的⊙D交BC延长线于点E.分析 (1)如图1中,设CM是两圆的公共弦,CM交BD于N,交OA于K,BD交⊙O于G,连接OC、CG交OA于H.首先证明OH是三角形中位线,根据△GCN∽△GOH,可得$\frac{CN}{OH}$=$\frac{CG}{OG}$,由此求出相关线段即可解决问题;
(2)只要证明△OCA∽△DCO,设AC=x,则有OC2=CA•CD,可得1=x(x+1),即可解决问题;
(3)首先证明BD=BE,再利用平行线的性质求出DG即可解决问题;
解答 解:(1)如图1中,设CM是两圆的公共弦,CM交BD于N,交OA于K,BD交⊙O于G,连接OC、CG交OA于H.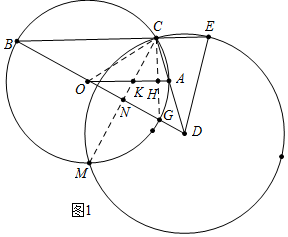
∵BG是直径,
∴∠BCG=90°,
∵BC∥OA,
∴∠OHG=∠BCG=90°,
∴OA⊥CG,
∴CH=HG,
∵CM⊥BD,
∴∠ONK=∠CHK=90°,∵∠OKN=∠CKH,
∴∠KON=∠KCH,
∵OG=OB,CH=HG,
∴OH=$\frac{1}{2}$BC=$\frac{4}{5}$,
∵OC=1,
∴CH=HG=$\sqrt{{1}^{2}-(\frac{4}{5})^{2}}$=$\frac{3}{5}$,
∵∠OGH=∠CGN,∠GCN=∠GOH,
∴△GCN∽△GOH,
∴$\frac{CN}{OH}$=$\frac{CG}{OG}$,
∴$\frac{CN}{\frac{4}{5}}$=$\frac{\frac{6}{5}}{1}$,
∴CN=$\frac{24}{25}$,
∴CM=2CN=$\frac{48}{25}$.
(2)如图2中,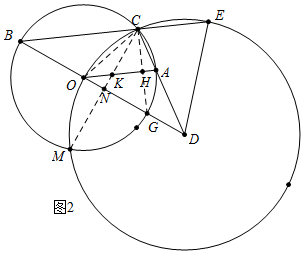
当△OAD是等腰三角形时,观察图形可知,只有OA=AD,
∴∠AOD=∠ADO=∠COA,
∵∠OCA=∠OCD,
∴△OCA∽△DCO,设AC=x,
则有OC2=CA•CD,
∴1=x(x+1),
∴x=$\frac{-1+\sqrt{5}}{2}$或$\frac{-1-\sqrt{5}}{2}$(舍弃),
∴CD=CA+AD=$\frac{\sqrt{5}+1}{2}$,
∵OA∥BC,
∴∠AOD=∠B=∠ODA,
∴BC=CD=$\frac{\sqrt{5}+1}{2}$.
(3)如图3中,作DN⊥CE于N.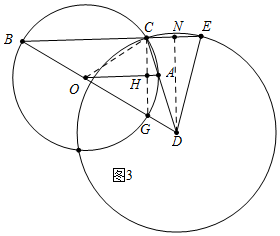
∵DC=DE,
∴∠DCE=∠E,
∵BC∥OA,
∴∠OAC=∠DCE=∠OCA,
∴∠AOC=∠CDE=∠B,
∴∠E=∠BDE,
∴BE=BD,
∵CG⊥BE,DN⊥BE,
∴CG∥DN,
∴$\frac{BG}{GD}$=$\frac{BC}{CN}$,
∴$\frac{2}{DG}$=$\frac{x}{\frac{y}{2}}$,
∴DG=$\frac{y}{x}$,
∵BD=BE,
∴2+$\frac{y}{x}$=x+y,
∴y=$\frac{2x-{x}^{2}}{x-1}$(1<x<2)
点评 本题考查圆综合题、垂径定理、勾股定理、平行线的性质、相似三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,正确寻找相似三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
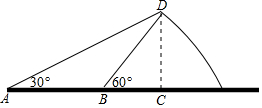 如图,由山脚下的一点A测得山顶D的仰角是30°,从A前进100米到B,再次测得山顶D的仰角为60°,求山高CD的高度(结果精确到0.1米).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,由山脚下的一点A测得山顶D的仰角是30°,从A前进100米到B,再次测得山顶D的仰角为60°,求山高CD的高度(结果精确到0.1米).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
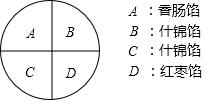 大年夜吃饺子是中华民族的传统习俗,妈妈为洋洋准备了四只饺子:一只香肠陷A,两只什锦馅B和C,一只红枣馅D,四只饺子除内部馅料不同外,其他均一切相同,洋洋喜欢吃什锦馅的饺子.
大年夜吃饺子是中华民族的传统习俗,妈妈为洋洋准备了四只饺子:一只香肠陷A,两只什锦馅B和C,一只红枣馅D,四只饺子除内部馅料不同外,其他均一切相同,洋洋喜欢吃什锦馅的饺子.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
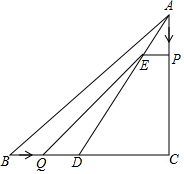 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在边BC上,且CD=3cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度沿AC向终点运动;点Q以1.25cm/s的速度沿BC向终点C运动,过点P作PE∥BC交AD于点E,连接EQ,设动点运动时间为ts(0<t<4).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在边BC上,且CD=3cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度沿AC向终点运动;点Q以1.25cm/s的速度沿BC向终点C运动,过点P作PE∥BC交AD于点E,连接EQ,设动点运动时间为ts(0<t<4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com